2015-03-22
622
Чтобы построить переходный процесс для нелинейности типа релейного звена, необходимо интегрировать дифференциальное уравнение на интервалах постоянства выхода нелинейного звена, причем начальными условиями каждого интервала (за исключением 1-го) являются конечные значения предыдущего интервала.
Начиная с 8-го уравнения для начального момента времени t=0 и заданных начальных условий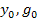 
определяют начальную ошибку.
Считаем, что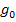 
изменилось в начальный момент времени скачкообразно: 
.
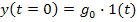Тогда
14) 
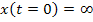(за счет дифференцирования ошибки, изменившейся скачкообразно)
15) 
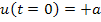
Т.о. управляющее воздействие на 1-м интервале равно +a.
I. x>b, u=+a
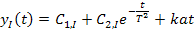
C1, C2 находим из начальных условий: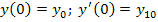 
.
Определив константы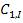 
, 
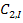, получим решение уравнения:
y
g0
t
xдиф
e xпроп
Как видно, функция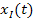 
, убывая, становится отрицательной, и когда она пересекает линию +b, управляющее воздействие на выходе нелинейного звена также становится равным нулю.
II. -b<x<b, u=0.
На втором интервале управление нулевое.
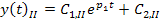
Для нахождения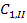 
, 
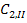воспользуемся условием совпадения значения функций и производных на границе 1-го и 2-го интервала:
|
|
|
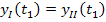
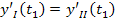
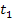– момент времени переключения реле, когда 
Определив постоянные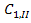 
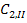, , продолжаем построение решения:
y
g0
b
| -b |
xдиф
e xпроп
Если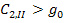 
, то с течением времени интегральная составляющая ошибки будет убывать, дифференциальная составляющая является отрицательной, и пропорциональная также отрицательна. За счет уменьшения интегральной составляющей переменная х в момент времени t2 станет x<-b, и произойдет переключение реле. На вход линейного звена будет подано управление –а.
III. x<-b, u=-a.
;
;
;
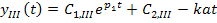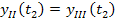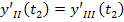Как видно, получение решения и исследование переходных процессов аналитическим методом достаточно сложно даже в случае кусочно-постоянных нелинейностей.
