Частным приращением функции  в точке
в точке  по переменной х называется выражение
по переменной х называется выражение 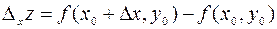 .
.
Частным приращением функции  в точке
в точке  по переменной у называется выражение
по переменной у называется выражение 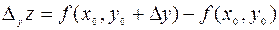 .
.
Частной производной от функции  по переменной х называется предел отношения частного приращения
по переменной х называется предел отношения частного приращения 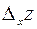 к приращению
к приращению 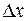 аргумента
аргумента 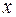 при стремлении
при стремлении 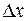 к нулю.
к нулю.
Обозначают частные производные одним из символов
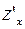 ,
, 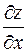 или
или 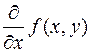 .
.
Итак, по определению 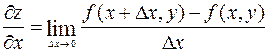 .
.
Аналогично определяется частная производная по переменной у:
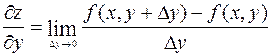 .
.
Из определения частных производных следует, что их нахождение сводится к обычному дифференцированию данной функции одной выделенной переменной при условии, что все остальные переменные считаются константами.
Пример. Найти частные производные функций:
а) 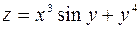 ,
,
б) 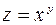 .
.
Решение. а) 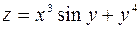 . Чтобы найти частную производную по
. Чтобы найти частную производную по 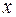 , считаем
, считаем 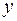 постоянной величиной. Таким образом,
постоянной величиной. Таким образом, 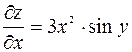 . Аналогично, дифференцируем по
. Аналогично, дифференцируем по 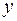 , считая
, считая 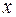 постоянной, находим частную производную по
постоянной, находим частную производную по 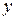 :
: 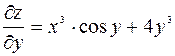 .
.
б) 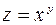 . При фиксированном
. При фиксированном 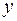 имеем степенную функцию от
имеем степенную функцию от 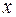 . Таким образом,
. Таким образом, 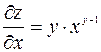 . При фиксированном
. При фиксированном 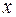 функция является показательной относительно
функция является показательной относительно 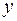 и
и 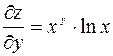 .
.
Функция  называется дифференцируемой в точке
называется дифференцируемой в точке  , если ее полное приращение в этой точке может быть представлено в виде
, если ее полное приращение в этой точке может быть представлено в виде
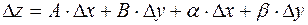 , (1)
, (1)
где 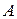 и
и 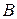 – некоторые числа;
– некоторые числа; 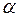 и
и 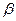 - бесконечно малые при
- бесконечно малые при 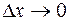 ,
, 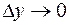 функции
функции 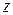 , то есть
, то есть 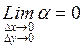 и
и 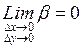 .
.
Теорема. Если функция  дифференцируема в точке
дифференцируема в точке 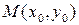 то она непрерывна в этой точке и имеет в ней частные производные по каждому аргументу
то она непрерывна в этой точке и имеет в ней частные производные по каждому аргументу 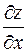 и
и 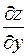 , причем
, причем 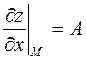 ,
, 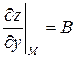 .
.
В силу теоремы, равенство (1) можно записать в виде
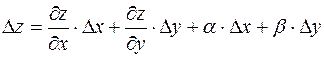 , (2)
, (2)
 2015-03-22
2015-03-22 301
301








