2015-03-22
336
П.В. Столбов
Математика
Часть II
Утверждено редакционно-издательским
советом университета в качестве
учебного пособия
Нижний Новгород
ННГАСУ
ББК 22.1
С 81
Столбов П.В. Математика. Часть II [текст]: учебное пособие / П.В. Столбов; Нижегород. гос. архит.-строит. ун-т.– Н.Новгород: ННГАСУ, 2012. – 62 с.
ISBN 978-5-87941-880-0
Учебное пособие и контрольные задания по математике предназначены для студентов заочной формы обучения всех специальностей.
ББК 22.1
ISBN 978-5-87941-880-0
© Столбов П.В., 2012
ФУНКЦИЯ ДВУХ ПЕРЕМЕННЫХ
Основные понятия
Функции одной независимой переменной не охватывают все зависимости, существующие в природе. Поэтому естественно расширить известное понятие функциональной зависимости и ввести понятие функции двух переменных, для которой можно дать наглядную геометрическую интерпретацию.
Пусть задано множество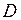 
упорядоченных пар чисел 
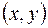плоскости 
.
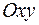Правило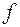 
, по которому каждой паре чисел 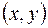множества 
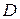ставится в соответствие одно и только одно действительное число 
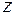называется функцией двух переменных, заданной на множестве 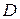со значениями в 
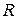и обозначается:
, 
.
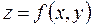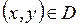Множество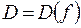 
называется областью определения функции. Множество значений, принимаемых 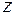в области определения, называется областью изменения этой функции и обозначается 
.
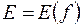При этом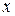 
и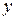 
называются независимыми переменными (аргументами), а 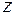– зависимой переменной (функцией).
Пример. Площадь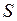 
прямоугольника со сторонами, длины которых равны 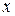и 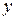является функцией двух переменных: 
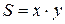. Область определения 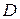этой функции 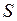есть множество 
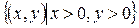. (См. рис. 1).
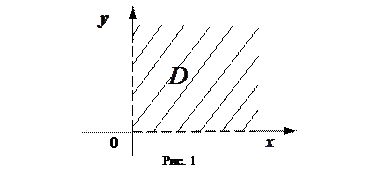
Функцию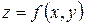 
, где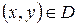 
можно рассматривать как функцию точки 
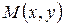координатной плоскости 
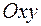. В частности, областью определения 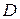может быть вся плоскость 
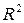или ее часть, ограниченная некоторыми линиями.
Пример. Найти область определения функции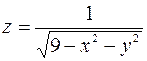 
.
Решение. Функция 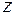существует для тех пар значени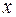й 
и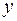 
, которые удовлетворяют неравенству 
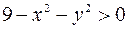или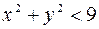 
, то есть представляет собой круг, не включая границу, с центром в начале координат и радиусом 
.
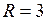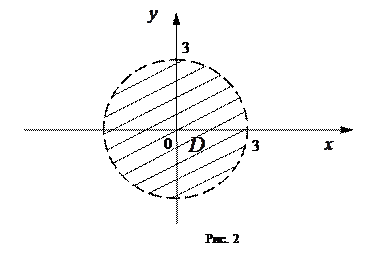
Графиком функции двух переменных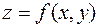 
называется множество точек 
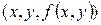трехмерного пространства, представляющее собой некоторую поверхность (рис. 3), которая геометрически изображает данную функцию 
.
|
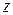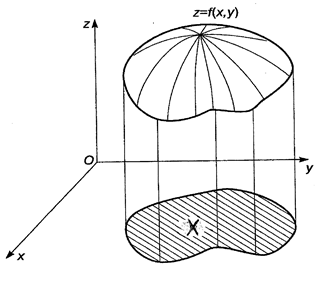
Рис. 3
Пример. Функция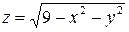 
имеет областью определения 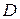замкнутый круг 
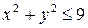и изображается верхней полусферой с центром в точке 
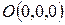и радиусом 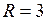(см. рис. 4).
Функция двух переменных, как и функция одной переменной, может быть задана различными способами: таблицей, аналитически, графиком. Будем пользоваться аналитическим способом: когда функция двух переменных задается с помощью формулы.
Как правило, построение поверхности оказывается довольно трудной задачей. Поэтому для изучения функции используют линии уровня. Понятие линии уровня широко используется, прежде всего, в геодезии, картографии, а также при описании различных физических полей (температура, давление и пр.).
Линией уровня функции двухпеременных 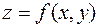называется кривая, 
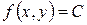на плоскости 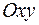в точках которой функция сохраняет постоянное значение 
.
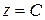Геометрически придание функции 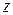постоянного значения 
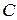означает пересечение поверхности 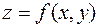с плоскостью 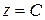, параллельной координатной плоскости .
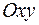Пример. Построить линии уровня функции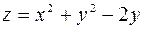 
.
Решение. Линии уровня данной функции – это семейство кривых на плоскости 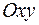, задаваемое уравнением 
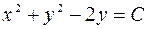или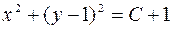 
. Это уравнение определяет семейство окружностей с центром в точке (0,1) и радиусом 
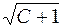; точка (0,1) – это вырожденная линия уровня, соответствующая минимальному значению функции 
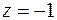(рис. 5).
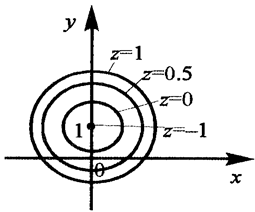
Рис. 5
