Большая часть понятий математического анализа, определенных ранее для функций одной переменной, может быть перенесена на случай двух переменных.
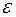 -окрестностью точки
-окрестностью точки 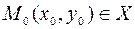 называется круг, с центром в точке
называется круг, с центром в точке 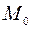 и радиусом
и радиусом 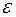 .
.
Пусть функция  определена в некоторой окрестности точки
определена в некоторой окрестности точки  , за исключением, может быть, самой этой точки. Число А называется пределом функции
, за исключением, может быть, самой этой точки. Число А называется пределом функции  при
при 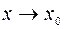 и
и 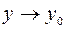 (или в точке
(или в точке  ), если для любого, сколь угодно малого положительного числа
), если для любого, сколь угодно малого положительного числа 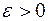 , найдется положительное число
, найдется положительное число 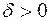 (зависящее от
(зависящее от 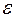 ), такое, что для всех точек из
), такое, что для всех точек из 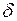 -окрестности точки
-окрестности точки  , выполняется неравенство
, выполняется неравенство 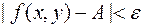 .
.
Обозначается предел так: 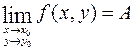 .
.
Геометрический смысл предела функции двух переменных состоит в следующем: каково бы ни было число 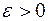 , найдется
, найдется 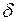 - окрестность точки
- окрестность точки  , что во всех ее точках
, что во всех ее точках 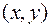 , отличных от
, отличных от  , аппликаты соответствующих точек поверхности
, аппликаты соответствующих точек поверхности  отличаются от числа А по модулю меньше, чем на
отличаются от числа А по модулю меньше, чем на 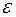 .
.
Пример. Найти предел 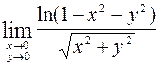 .
.
Решение. Обозначим 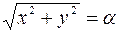 . Условие
. Условие 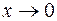 ,
, 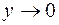 равносильно тому, что
равносильно тому, что 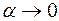 . Тогда данный предел запишется в виде
. Тогда данный предел запишется в виде

неопределенность раскрывается по правилу Лопиталя
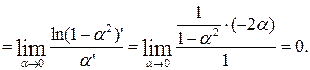
Полным приращением функции  в точке
в точке  называется выражение
называется выражение 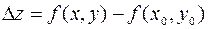 , где
, где 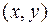 - любая точка из области определения функции.
- любая точка из области определения функции.
Обозначим 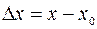 ,
, 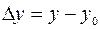 , тогда
, тогда
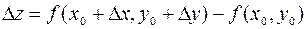 .
.
Функция  называется непрерывной в точке
называется непрерывной в точке 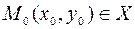 , если ее полное приращение в этой точке стремится к нулю при
, если ее полное приращение в этой точке стремится к нулю при 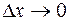 и
и 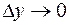 , то есть
, то есть 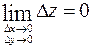 .
.
 2015-03-22
2015-03-22 353
353








