Пусть задана функция  , где переменные
, где переменные 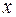 и
и 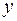 , в свою очередь, являются функциями независимой переменной
, в свою очередь, являются функциями независимой переменной 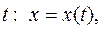 .
. 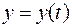 Тогда функция
Тогда функция 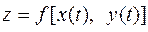 будет сложной функцией независимой переменной
будет сложной функцией независимой переменной 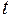 , а переменные
, а переменные 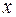 и
и 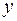 будут для нее промежуточными переменными.
будут для нее промежуточными переменными.
Теорема. Если функции 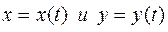 дифференцируемы в точке
дифференцируемы в точке 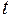 , а функция
, а функция  дифференцируема в точке
дифференцируема в точке 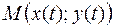 , то сложная функция
, то сложная функция 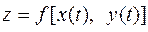 также дифференцируема в точке
также дифференцируема в точке 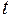 , причем
, причем
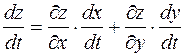 . (1)
. (1)
Пример. Найти 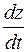 , где
, где 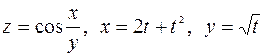 .
.
Решение. Найдем сначала 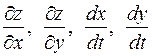 :
:
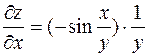 ,
, 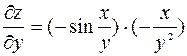 ,
,
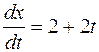 ,
, 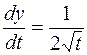 .
.
Тогда, согласно формуле (1), имеем
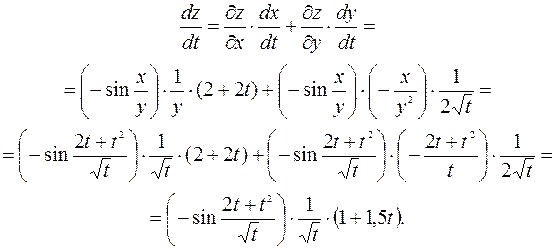

 2015-03-22
2015-03-22 295
295








