Рассмотрим произведение трех векторов  ,
,  и
и 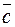 , составленное следующим образом:
, составленное следующим образом: 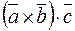 , то есть первые два вектора
, то есть первые два вектора  и
и  умножаются векторно, а их результат скалярно на третий вектор
умножаются векторно, а их результат скалярно на третий вектор 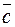 . Такое произведение векторов называется векторно-скалярным или смешанным и обозначается
. Такое произведение векторов называется векторно-скалярным или смешанным и обозначается 

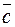 , то есть
, то есть 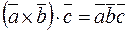 .
.
Смешанное произведение трех векторов  ,
,  и
и  представляет собой число, равное объему параллелепипеда, построенного на этих векторах (см. рис. 11), взятое со знаком «плюс», если эти три вектора образуют правую тройку и со знаком «минус», если они образуют левую тройку векторов.
представляет собой число, равное объему параллелепипеда, построенного на этих векторах (см. рис. 11), взятое со знаком «плюс», если эти три вектора образуют правую тройку и со знаком «минус», если они образуют левую тройку векторов.
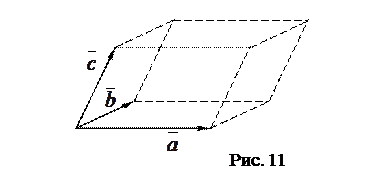
Свойства смешанного произведения:
1) 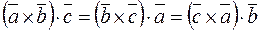 ;
;
2) 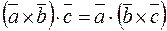 ;
;
3) 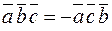 ;
; 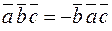 ,
, 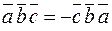 ;
;
4) Если 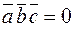 , то векторы
, то векторы  ,
,  и
и 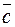 компланарны.
компланарны.
Смешанное произведение трех векторов  ,
,  и
и 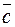 заданных своими координатами, то есть
заданных своими координатами, то есть 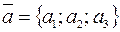 ,
, 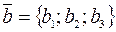 ,
, 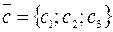 вычисляется по формуле:
вычисляется по формуле:
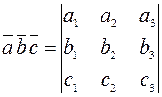 .
.
Пример. Вычислить смешанное произведение векторов 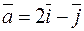 ,
, 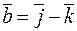 ,
, 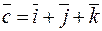 .
.
 2015-03-22
2015-03-22 353
353








