Пусть задана функция  и можно вычислить
и можно вычислить 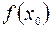 , то есть значение этой функции в точке
, то есть значение этой функции в точке  . Требуется вычислить значение этой функции
. Требуется вычислить значение этой функции  в точке
в точке 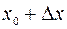 .
.
Если данная функция  дифференцируема в точке
дифференцируема в точке  , то в точке
, то в точке 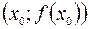 существует касательная
существует касательная 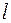 к графику функции
к графику функции  (см. рис. 56). Тогда приращение функции
(см. рис. 56). Тогда приращение функции 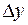 можно представить в виде:
можно представить в виде:
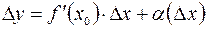 .
.
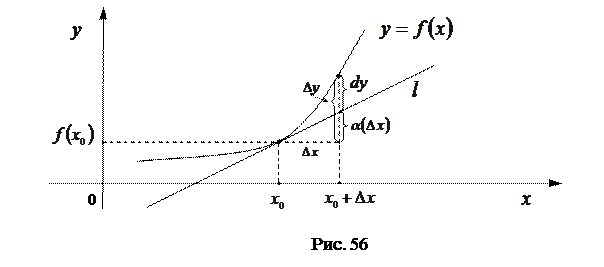
Главную часть линейную относительно приращения 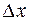 независимой переменной
независимой переменной 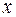 в последнем равенстве, то есть выражение
в последнем равенстве, то есть выражение 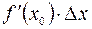 называют дифференциалом функции
называют дифференциалом функции  в точке
в точке  и обозначают
и обозначают 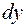 . Итак,
. Итак, 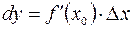 .
.
При 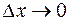 , то есть при
, то есть при 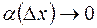 приращение функции
приращение функции 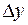 приближенно равно дифференциалу
приближенно равно дифференциалу 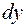 :
:
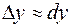 или
или 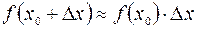 .
.
Последнюю формулу применяют для приближенного вычисления значений функций в точке.
Пример. Вычислить 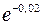 .
.
Решение. Рассмотрим функцию 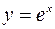 . Пусть
. Пусть 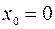 , тогда
, тогда 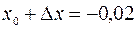 , откуда
, откуда 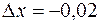 .
.
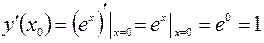 ,
,
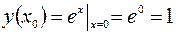 .
.
Следовательно, 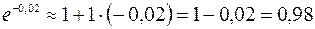 .
.
Ответ: 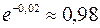 .
.
Заметим, что дифференциал независимой переменной равен ее приращению, то есть 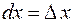 , так как
, так как 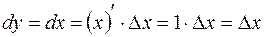 . Таким образом, дифференциал функции вычисляется по формуле:
. Таким образом, дифференциал функции вычисляется по формуле:
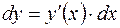 .
.
Пример. Найти дифференциал функции 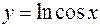 .
.
Решение. 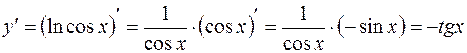 , тогда
, тогда 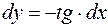 .
.
 2015-03-22
2015-03-22 668
668








