1. Областью определения 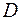 данной функции
данной функции  является множество всех действительных чисел
является множество всех действительных чисел 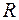 , кроме
, кроме 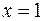 , то есть
, то есть 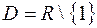 .
.
2. Поскольку 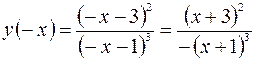 и
и 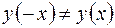 и
и 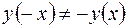 , то функция
, то функция  не является четной и нечетной, то есть данная функция
не является четной и нечетной, то есть данная функция  общего вида.
общего вида.
3. Находим асимптоты кривой.
Поскольку 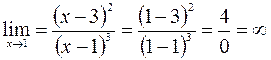 , то
, то 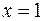 – уравнение вертикальной асимптоты графика данной функции
– уравнение вертикальной асимптоты графика данной функции  .
.
Наклонные асимптоты находим в виде уравнения прямой 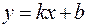 :
:
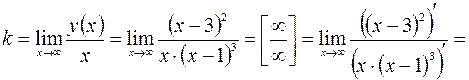
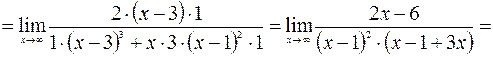
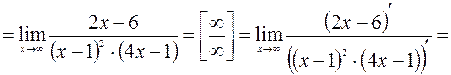
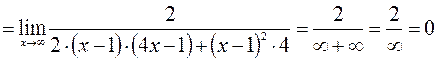 ;
;
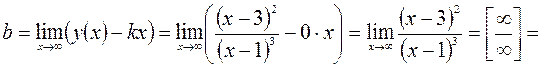
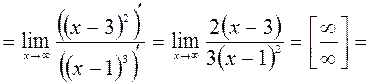
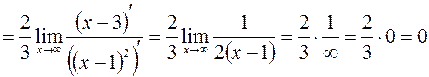 .
.
Следовательно 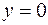 – уравнение горизонтальной асимптоты графика данной функции
– уравнение горизонтальной асимптоты графика данной функции  .
.
4. Находим интервалы монотонности и точки экстремума функции.
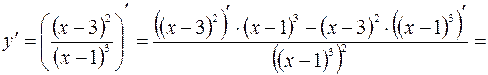
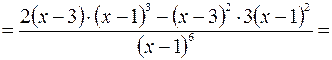
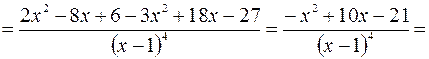
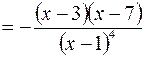
Используя необходимое условие экстремума, находим 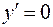
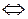
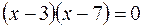 , откуда
, откуда 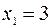 или
или 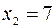 ;
; 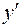 не существует
не существует 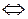
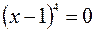 , откуда
, откуда 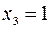 .
.
Используем достаточные условия экстремума. Найденные три критические точки наносим на область определения 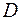 и определяем знак
и определяем знак 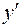 в каждом из четырех интервалов.
в каждом из четырех интервалов.
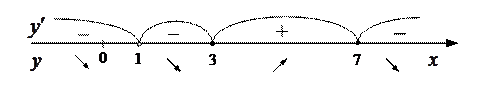
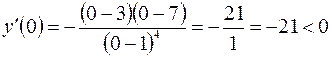
Так как 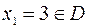 и при переходе через эту точку
и при переходе через эту точку 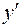 меняет знак минус на плюс, то
меняет знак минус на плюс, то 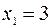 – точка минимума функции
– точка минимума функции  ,
, 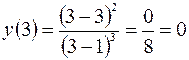 .
.
Так как 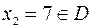 и при переходе через эту точку
и при переходе через эту точку 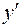 меняет знак плюс на минус, то
меняет знак плюс на минус, то 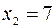 – точка максимума функции
– точка максимума функции  ,
, 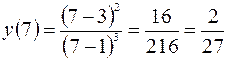 .
.
Так как при 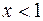 ,
, 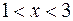 ,
, 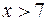
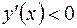 , то в интервалах
, то в интервалах 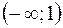 ,
, 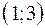 ,
, 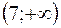 функция
функция  монотонно убывает.
монотонно убывает.
Так как при 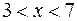
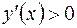 , то в интервале
, то в интервале 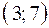 функция
функция  монотонно возрастает.
монотонно возрастает.
5. Находим интервалы выпуклости (вогнутости) кривой и точки перегиба.
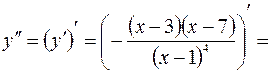
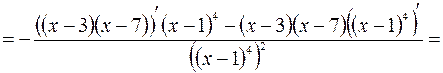
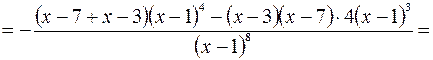
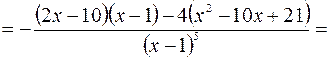
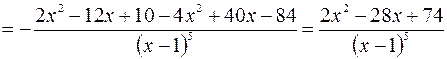 .
.
Итак, 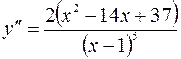 .
.
Используя необходимое условие перегиба, находим 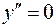
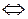
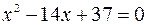 , или
, или 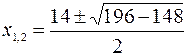 , откуда
, откуда 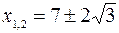 ;
; 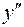 не существует
не существует 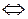
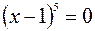 , откуда
, откуда 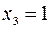 .
.
Используем достаточные условия перегиба.
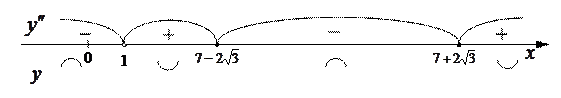
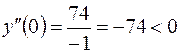 .
.
Так как точки 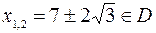 и при переходе через эти точки
и при переходе через эти точки 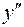 меняет знак, то
меняет знак, то 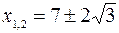 – точки перегиба графика функции
– точки перегиба графика функции  .
.
Так как при 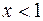 ,
, 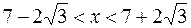
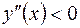 , то в интервалах
, то в интервалах 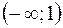 ,
, 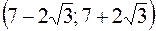 функция
функция  выпукла вниз.
выпукла вниз.
Так как при 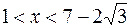 ,
, 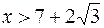
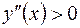 , то в интервалах
, то в интервалах 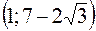 ,
, 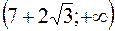 функция
функция  выпукла вверх.
выпукла вверх.
6. Находим координаты точек пересечения кривой с координатными осями:
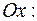
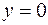
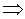
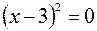 , откуда
, откуда 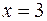 ;
;
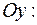
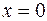
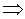
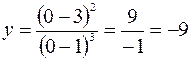 .
.
7. Строим эскиз графика данной функции. (См. рис. 65).
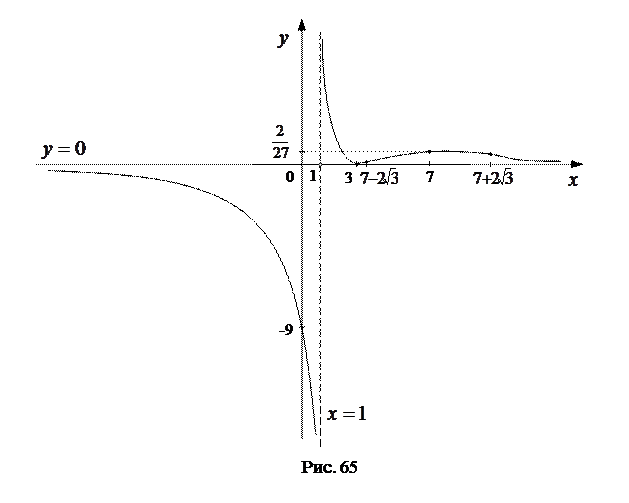
 2015-03-22
2015-03-22 886
886








