2015-03-22
512
Функция вида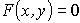 
называется неявной. Дифференцируя обе части этого тождества по х (пользуясь правилом дифференцирования сложной функции), считая, что y есть функция от x, получим уравнение первой степени относительно y'. Из этого уравнения легко находят y'.
Пример.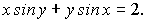 
Решение: Дифференцируя по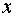 
обе части уравнения, получим
;
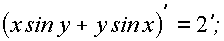
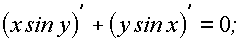
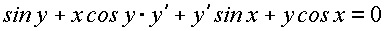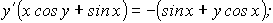
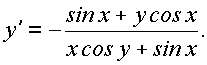
42. Производные и дифференциалы высших порядков.
Производные высших порядков
Если функция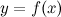 
имеет производную в каждой точке 
своей области определения, то ее производная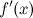 
есть функция от . Функция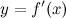 
, в свою очередь, может иметь производную, которую называют производной второго порядка функции 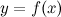(или второй производной) и обозначают символом 
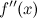. Таким образом
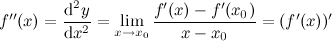
43. Теоремы Ферма, Ролля и Коши. Теорема Лагранжа.
Теорема Ферма. (О равенстве нулю производной)
Пусть функция 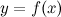удовлетворяет следующим условиям:
- она дифференцируема на интервале
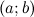; - достигает наибольшего или наименьшего значения в точке
.
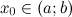Тогда производная в этой точке равна нулю, то есть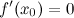 
.
Следствие. (Геометрический смысл теоремы Ферма)
В точке наибольшего и наименьшего значения, достигаемого внутри промежутка, касательная к графику функции параллельна оси абсцисс.
