Элементы линейной алгебры.
51-60. Дана система линейных уравнений
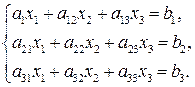
Доказать ее совместимость и решить двумя способами: 1) методом Гаусса; 2) средствами матричного исчисления.
51. 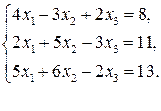 56.
56. 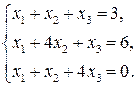
52. 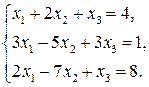 57.
57. 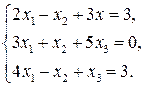
53. 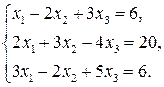 58.
58. 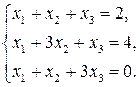
54. 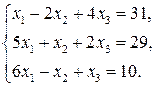 59.
59. 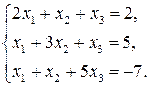
55. 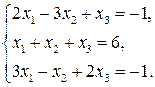 60.
60. 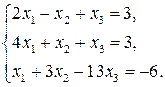
61-70. Даны два линейных преобразования:
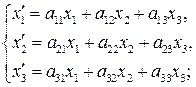
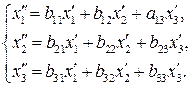
Средствами матричного исчисления найти преобразование, выражающее
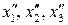 через
через 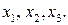
61. 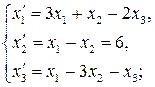
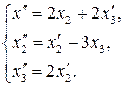
62. 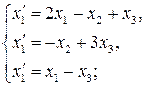
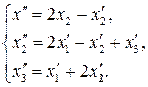
63. 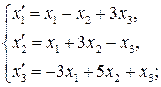
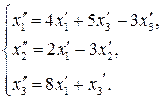
64. 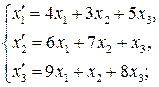
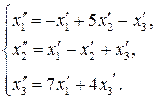
65. 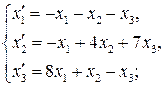
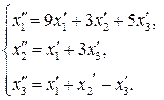
66. 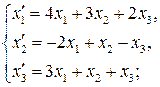
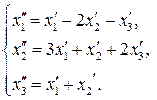
67. 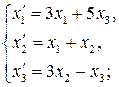
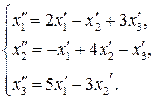
68. 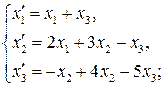
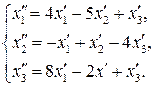
69. 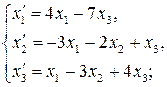
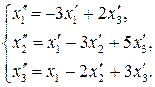
70 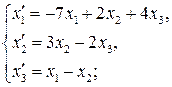
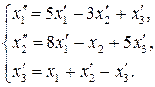
71-80. Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей 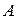 .
.
71. 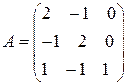 . 76.
. 76. 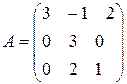 .
.
72. 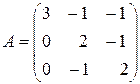 . 77.
. 77. 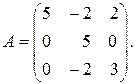
73. 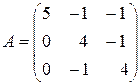 . 78.
. 78. 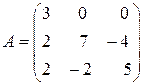 .
.
74. 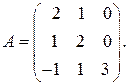 79.
79. 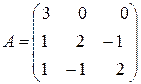 .
.
75. 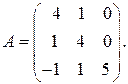 80.
80. 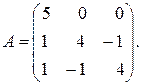
81-90. Используя теорию квадратичных форм, привести к каноническому виду уравнение линии второго порядка.
81. 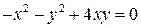 . 86.
. 86. 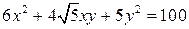 .
.
82. 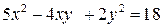 . 87.
. 87. 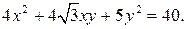
83. 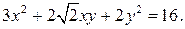 88.
88. 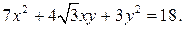
84. 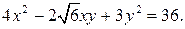 89.
89. 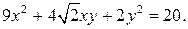
85. 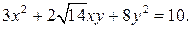 90.
90. 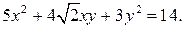
91-100. Дано комплексное число 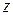 . Требуется: 1) записать его в алгебраической и тригонометрической формах; 2) найти все корни уравнения
. Требуется: 1) записать его в алгебраической и тригонометрической формах; 2) найти все корни уравнения 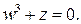
91. 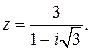 96.
96. 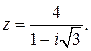
92. 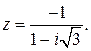 97.
97. 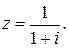
93. 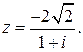 98.
98. 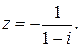
94. 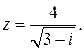 99.
99. 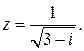
95. 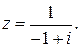 100.
100. 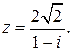
Введение в математический анализ
101-110. а) Найти область определения функции; б), в) построить графики функции при помощи преобразований графиков основных элементарных функций.
101. а) 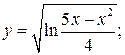 б)
б) 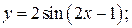 в)
в) 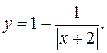
102. а) 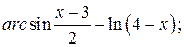 б)
б) 
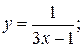 в)
в) 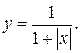
103. а) 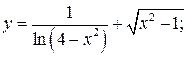 б)
б) 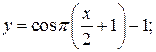 в)
в) 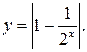
104. а) 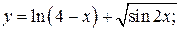 б)
б) 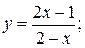 в)
в) 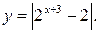
105. а) 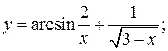 б)
б) 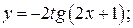 в)
в) 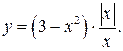
106. а) 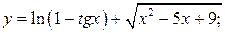 б)
б) 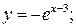 в)
в) 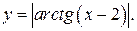
107. а) 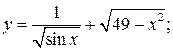 б)
б) 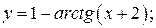 в)
в) 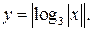
108. а) 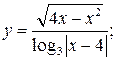 б)
б) 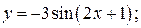 в)
в) 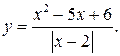
109. а) 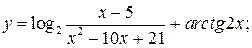 б)
б) 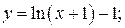 в)
в) 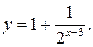
110. а) 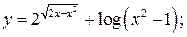 б)
б) 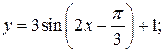 в)
в) 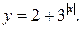
111-120. Найти пределы функций, не пользуясь правилом Лопиталя.
111. а) 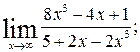 б)
б) 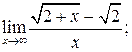
в) 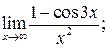 г)
г) 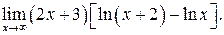
112. а) 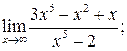 б)
б) 
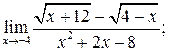
в) 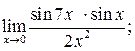 г)
г) 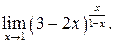
113. а) 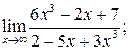 б)
б) 
в) 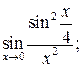 г)
г) 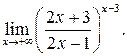
114. а) 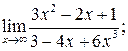 б)
б) 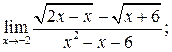
в) 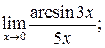 г)
г) 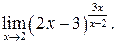
115. а) 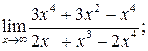 б)
б) 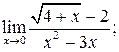
в) 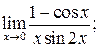 г)
г) 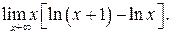
116. а) 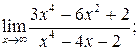 б)
б) 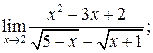
в) 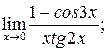 г)
г) 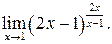
117. а) 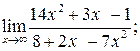 б)
б) 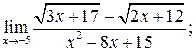
в) 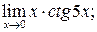 г)
г) 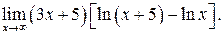
118. а) 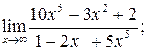 б)
б) 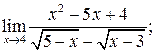
в) 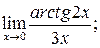 г)
г) 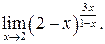
119. а) 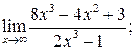 б)
б) 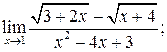
в) 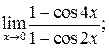 г)
г) 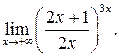
120. 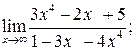 б)
б) 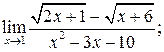
в) 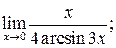 г)
г) 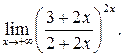
121-130. Заданы функция 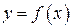 и два значения аргумента
и два значения аргумента 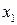 и
и 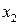 . Требуется: 1) установить, является ли данная функция непрерывной или разрывной для каждого из заданных значений аргумента; 2) в случае разрыва функции найти ее пределы слева и справа; 3) сделать схематический чертеж.
. Требуется: 1) установить, является ли данная функция непрерывной или разрывной для каждого из заданных значений аргумента; 2) в случае разрыва функции найти ее пределы слева и справа; 3) сделать схематический чертеж.
121. 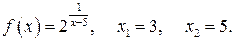 126.
126. 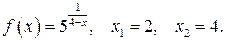
122. 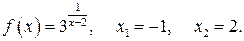 127.
127. 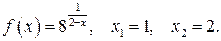
123. 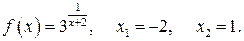 128.
128. 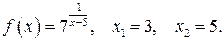
124. 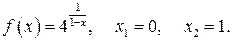 129.
129. 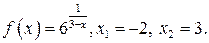
125. 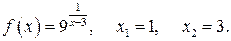 130.
130. 
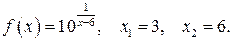
131-140. Задана функция 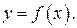 Найти точки разрыва, если они существуют. Сделать схематический чертеж.
Найти точки разрыва, если они существуют. Сделать схематический чертеж.
131. 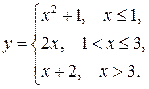 136.
136. 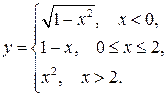
132. 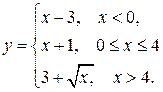 137.
137. 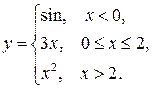
133. 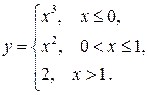 138.
138. 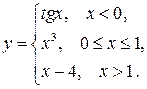
134. 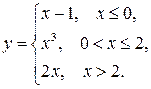 139.
139. 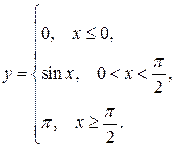
135. 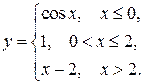
140. 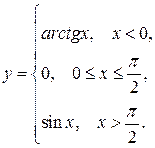
4. Производная и ее приложения
141-150. Найти производные 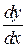 данных функций.
данных функций.
141. а) 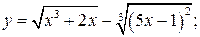 б)
б) 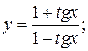
в) 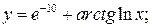 г)
г) 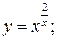
д) 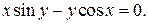
142. а) 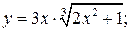 б)
б) 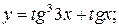
в) 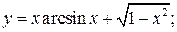 г)
г) 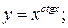
д) 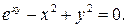
143. а) 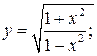 б)
б) 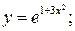
в) 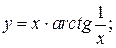 г)
г) 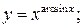
д) 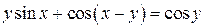
144. а) 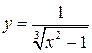 ; б)
; б) 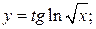
в) 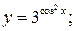 г)
г) 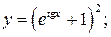
д) 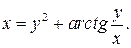
145. а) 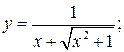 : б)
: б) 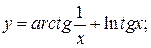
в) 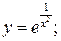 г)
г) 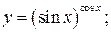
д) 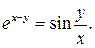
146. а) 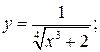 б)
б) 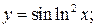
в) 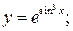 г)
г) 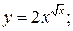
д) 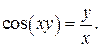
147. а) 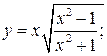 б)
б) 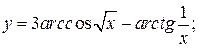
в) 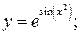 г)
г) 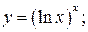
д) 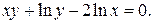
148. а) 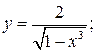 б)
б) 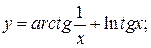
в) 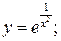 г)
г) 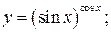
д) 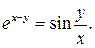
149. а) 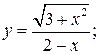 б)
б) 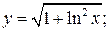
в) 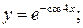 г)
г) 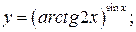
д) 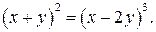
150. а) 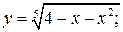 б)
б) 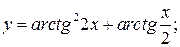
в) 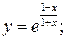 г)
г) 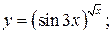
д) 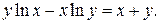
151-160. Найти производное первого и второго порядка от заданных функций.
151. а) 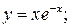 б)
б) 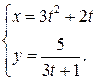
152. а) 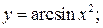 б)
б) 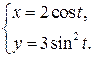
153. а) 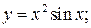 б)
б) 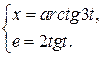
154. а) 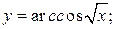 б)
б) 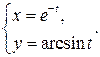
155. а) 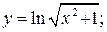 б)
б) 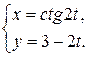
156. а) 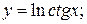 б)
б) 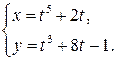
157. а) 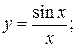 б)
б) 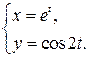
158. а) 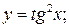 б)
б) 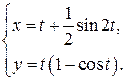
159. а) 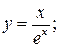 б)
б) 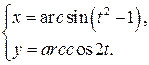
160. а) 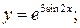 б)
б) 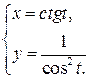
161-170. Применяя формулу Тейлора с остаточным членом в форме Лагранжа к функции 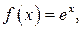 вычислить значение
вычислить значение  с точностью до 0,001.
с точностью до 0,001.
161. 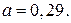 162.
162. 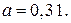 163.
163. 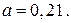 164.
164. 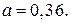 165.
165. 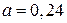
166. 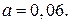 167.
167. 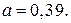 168.
168. 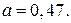 169.
169. 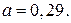 170.
170. 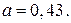
171-180. Найти наибольшее и наименьшее значения функции 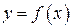 на отрезке
на отрезке 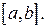
171. 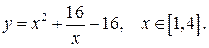 176.
176. 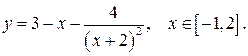
172. 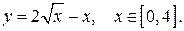 177.
177. 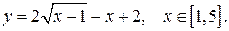
173. 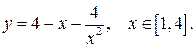 178.
178. 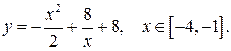
174. 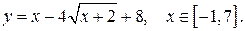 179.
179. 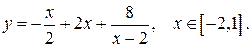
175. 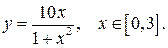 180.
180. 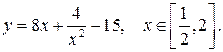
181. Требуется изготовить ящик с крышкой, объём которого был бы равен 72 см 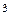 , причем стороны основания относились бы как 1:2. Каковы должны быть размеры всех сторон, чтобы полная поверхность была наименьшей?
, причем стороны основания относились бы как 1:2. Каковы должны быть размеры всех сторон, чтобы полная поверхность была наименьшей?
182. Объём правильной треугольной призмы равен 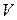 . Какова должна быть сторона основания, чтобы полная поверхность призмы была наименьшей?
. Какова должна быть сторона основания, чтобы полная поверхность призмы была наименьшей?
183. Открытый чан объема 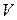 имеет форму цилиндра. Каковы должна быть радиус основания и высота цилиндра, чтобы его поверхность была наименьшей?
имеет форму цилиндра. Каковы должна быть радиус основания и высота цилиндра, чтобы его поверхность была наименьшей?
184. Найти соотношение между радиусом 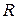 и высотой
и высотой 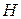 цилиндра, имеющего при данном объёме наименьшую полную поверхность.
цилиндра, имеющего при данном объёме наименьшую полную поверхность.
185. Требуется изготовить коническую воронку с образующей, равной 20 см. Какова должна высота воронки, чтобы её объём был наибольший?
186. Периметр равнобедренного треугольника равен 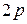 . Каковы должны быть его стороны, чтобы объём конуса, образованного вращением этого треугольника вокруг его основания, был наибольшим?
. Каковы должны быть его стороны, чтобы объём конуса, образованного вращением этого треугольника вокруг его основания, был наибольшим?
187. Периметр равнобедренного треугольника равен 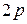 . Каковы должны быть его стороны, чтобы объём конуса, образованного вращением этого треугольника вокруг его высоты, был наибольшим?
. Каковы должны быть его стороны, чтобы объём конуса, образованного вращением этого треугольника вокруг его высоты, был наибольшим?
188. Найти высоту цилиндра наибольшего объёма, который можно вписать в шар радиуса 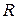 .
.
189. Найти высоту конуса наибольшего объёма, который можно вписать в шар радиуса 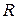 .
.
190. Полотняный шатер объёмом 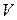 имеет форму прямого кругового конуса. Каково должно быть отношение высоты конуса к радиусу основания, чтобы на шатер ушло наименьшее количество полотна?
имеет форму прямого кругового конуса. Каково должно быть отношение высоты конуса к радиусу основания, чтобы на шатер ушло наименьшее количество полотна?
Приложения дифференциального исчисления
191-210. Исследовать функцию методами дифференциального исчисления и построить её график.
191. 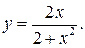 201.
201. 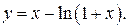
192. 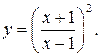 202.
202. 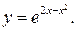
193. 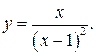 203.
203. 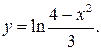
194. 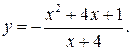 204.
204. 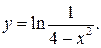
195. 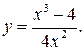 205.
205. 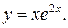
196. 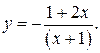 206.
206. 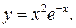
197. 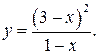 207.
207. 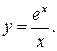
198. 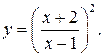 208.
208. 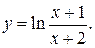
199. 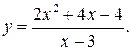 209.
209. 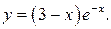
200. 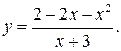 210.
210. 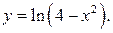
211-220. Найти уравнения касательной, уравнение нормальной плоскости и вычислить кривизну линии 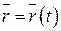 в точке
в точке 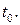
211. 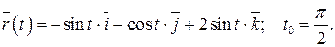
212. 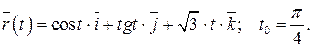
213. 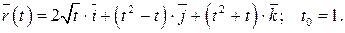
214. 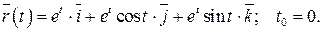
215. 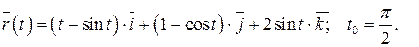
216. 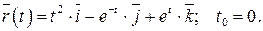
217. 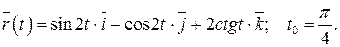
218. 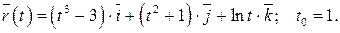
219. 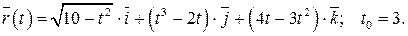
220. 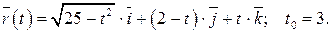
221-230. Определить число действительных корней уравнения 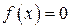 , отделить корни и, применяя комбинированный метод хорд и касательных, найти их приближенные значения.
, отделить корни и, применяя комбинированный метод хорд и касательных, найти их приближенные значения.
221. 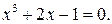 226.
226. 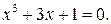
222. 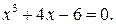 227.
227. 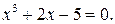
223. 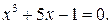 228.
228. 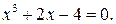
224. 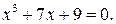 229.
229. 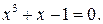
225. 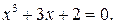 230.
230. 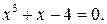
 2015-03-22
2015-03-22 1142
1142







