Экстремум функции нескольких переменных

Определение 10.1. Функция 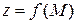имеет в точке локальный максимум (минимум), если найдется такая 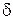-окрестность точки , в пределах которой значение 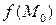является наибольшим (наименьшим) из всех значений 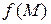этой функции.

Определение 10.2. Функция 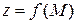имеет в точке локальный экстремум, если она имеет в этой точке либо локальный максимум, либо локальный минимум.

Условия локального экстремума функции 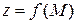, имеющей в точке частные производные первого порядка по всем переменным, дает следующая теорема.

Теорема. Если функция 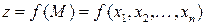имеет в точке 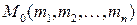частные производные первого порядка по всем переменным 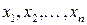и имеет в этой точке локальный экстремум, то все частные производные первого порядка обращаются в точке в нуль, т. е.

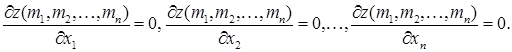
Точки, в которых все частные производные первого порядка функции 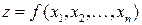обращаются в нуль, называют стационарными точками этой функции.

В каждой стационарной точке функции 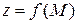возможен локальный экстремум, однако его существование можно установить лишь с помощью достаточных условий. Сформулируем эти условия.

Второй дифференциал функции 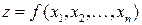в точке можно записать в виде

.

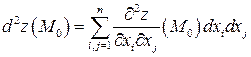Это выражение представляет собой квадратичную форму от переменных 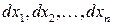, коэффициентами которой являются частные производные второго порядка.