Пусть функция 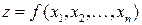 дифференцируема в некоторой окрестности точки
дифференцируема в некоторой окрестности точки 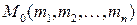 и дважды дифференцируема в самой точке
и дважды дифференцируема в самой точке  , причем точка
, причем точка  – точка возможного экстремума данной функции, т. е.
– точка возможного экстремума данной функции, т. е. 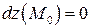 . Тогда если второй дифференциал
. Тогда если второй дифференциал 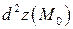 является положительно определенной (отрицательно определенной) квадратичной формой от переменных
является положительно определенной (отрицательно определенной) квадратичной формой от переменных 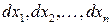 , то функция
, то функция 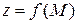 имеет в точке
имеет в точке  локальный минимум (максимум). Если же
локальный минимум (максимум). Если же 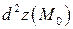 является знакопеременной квадратичной формой, то в точке
является знакопеременной квадратичной формой, то в точке  функция не имеет локального экстремума.
функция не имеет локального экстремума.
Рассмотрим случай двух переменных. Пусть функция 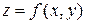 дифференцируема в некоторой окрестности точки
дифференцируема в некоторой окрестности точки 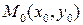 и дважды дифференцируема в самой точке
и дважды дифференцируема в самой точке  , причем точка
, причем точка  – точка возможного экстремума данной функции, т. е.
– точка возможного экстремума данной функции, т. е. 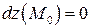 . Введем обозначения:
. Введем обозначения:
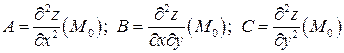 .
.
Тогда на основе вышесказанного и критерия Сильвестра знакоопределенности квадратичной формы, известного из курса линейной алгебры, следуют такие выводы:
1) если 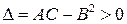 , то в точке
, то в точке  функция
функция 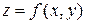 имеет локальный экстремум, причем максимум, если
имеет локальный экстремум, причем максимум, если 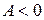 и минимум, если
и минимум, если 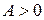 ;
;
2) если 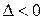 , то в точке
, то в точке  функция
функция 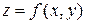 не имеет локального экстремума;
не имеет локального экстремума;
3) если 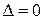 , то в точке
, то в точке  функция
функция 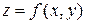 может иметь локальный экстремум, а может и не иметь его.
может иметь локальный экстремум, а может и не иметь его.
Обратимся к определению условного экстремума. Рассмотрим функцию 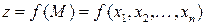 при условии, что ее аргументы связаны между собой соотношениями
при условии, что ее аргументы связаны между собой соотношениями 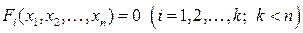 . Последние называют условиями связи. Пусть координаты точки
. Последние называют условиями связи. Пусть координаты точки 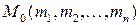 удовлетворяют условиям связи.
удовлетворяют условиям связи.
Определение 10.3. Функция 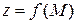 имеет в точке
имеет в точке  условный минимум (максимум) при условии связи
условный минимум (максимум) при условии связи 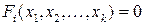
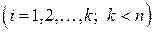 , если найдется такая
, если найдется такая 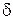 -окрестность точки
-окрестность точки  , в пределах которой значение
, в пределах которой значение 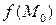 является наименьшим (наибольшим) из всех значений
является наименьшим (наибольшим) из всех значений 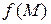 этой функции, т. е. выполняется неравенство
этой функции, т. е. выполняется неравенство
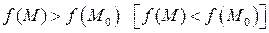 .
.
Другими словами, условный минимум (максимум) – это наименьшее (наибольшее) значение функции в точке  по отношению не ко всем точкам из некоторой окрестности точки
по отношению не ко всем точкам из некоторой окрестности точки  , а только к тем из них, которые связаны между собой условиями связи.
, а только к тем из них, которые связаны между собой условиями связи.
Рассмотрим два метода нахождения точек условного экстремума.
1. Метод исключения. Если уравнения связи
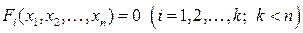
удается разрешить относительно каких-то 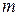 переменных, например относительно переменных
переменных, например относительно переменных 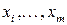 , т. е.
, т. е.
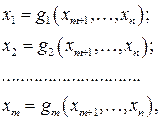
то исследование функции 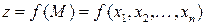 на условный экстремум при ограничениях
на условный экстремум при ограничениях 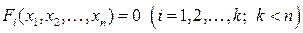 сводится к исследованию на обычный (безусловный) экстремум функции
сводится к исследованию на обычный (безусловный) экстремум функции 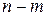 переменных
переменных 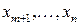 :
:
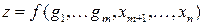 .
.
2. Метод Лагранжа. Пусть функции
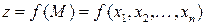 ,
, 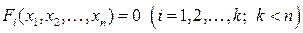
непрерывно дифференцируемы в окрестности точки  и ранг матрицы Якоби
и ранг матрицы Якоби
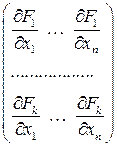
в этой точке равен 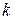 . Функцию
. Функцию
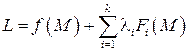
называют функцией Лагранжа, параметры 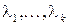 называют множителями Лагранжа. Сформулируем необходимые и достаточные условия существования условного экстремума.
называют множителями Лагранжа. Сформулируем необходимые и достаточные условия существования условного экстремума.
Необходимые условия. Для того чтобы точка  являлась точкой условного экстремума функции
являлась точкой условного экстремума функции 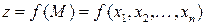 при уравнениях связи
при уравнениях связи 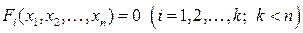 , необходимо, чтобы ее координаты при некоторых значениях
, необходимо, чтобы ее координаты при некоторых значениях 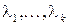 удовлетворяли системе уравнений
удовлетворяли системе уравнений
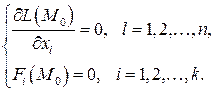
Достаточные условия. Пусть функции
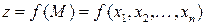 ,
, 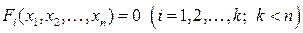
дважды непрерывно дифференцируемы в окрестности точки  , а также пусть в этой точке выполняются необходимые условия существования условного экстремума функции
, а также пусть в этой точке выполняются необходимые условия существования условного экстремума функции 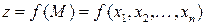 при
при
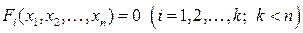 .
.
Тогда если при выполнении условий
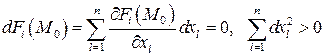
второй дифференциал 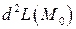 функции Лагранжа является положительно (отрицательно) определенной квадратичной формой, то функция
функции Лагранжа является положительно (отрицательно) определенной квадратичной формой, то функция 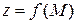 в точке
в точке  имеет условный строгий минимум (максимум). Если второй дифференциал
имеет условный строгий минимум (максимум). Если второй дифференциал 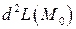 является неопределенной квадратичной формой, то в точке
является неопределенной квадратичной формой, то в точке  условного экстремума нет.
условного экстремума нет.
Если функция непрерывна на замкнутом ограниченном множестве 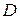 , то она достигает на нем наибольшего и наименьшего значений. Эти значения она может принимать как во внутренних точках множества
, то она достигает на нем наибольшего и наименьшего значений. Эти значения она может принимать как во внутренних точках множества 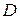 (точки экстремума), так и на его границе. Следовательно, необходимо специальное исследование граничных точек множества.
(точки экстремума), так и на его границе. Следовательно, необходимо специальное исследование граничных точек множества.
Пример 10.1. Исследовать функцию 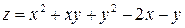 на экстремум.
на экстремум.
Решение. Найдём стационарные точки из системы уравнений:
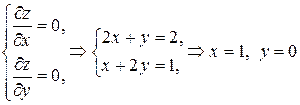 .
.
Имеется одна стационарная точка 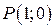 . Выясним, является ли эта точка точкой экстремума. Найдём вторые производные:
. Выясним, является ли эта точка точкой экстремума. Найдём вторые производные:
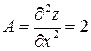 ;
; 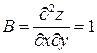 ;
; 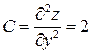 ;
; 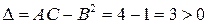 .
.
Так как 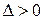 , то в точке
, то в точке 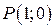 есть экстремум. Поскольку
есть экстремум. Поскольку 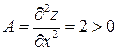 , то в точке
, то в точке 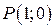 функция имеет локальный минимум, равный
функция имеет локальный минимум, равный 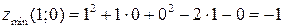 .
.
Пример 10.2. Исследовать на экстремум функцию трех переменных
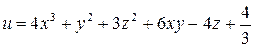 .
.
Решение. Найдем частные производные первого порядка:
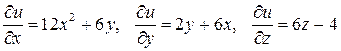 .
.
Решив систему
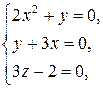
найдем стационарные точки 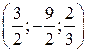 и
и 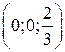 .
.
Вычислим частные производные второго порядка:
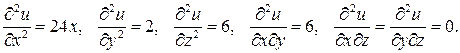
Составим матрицу второго дифференциала функции:
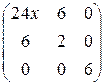 .
.
В точке 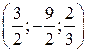 ее главные миноры
ее главные миноры
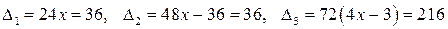
положительны. Следовательно, в этой точке функция имеет минимум 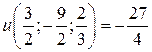 . Для исследования функции в точке
. Для исследования функции в точке 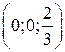 нельзя использовать критерий Сильвестра, т. к.
нельзя использовать критерий Сильвестра, т. к. 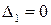 . В этой точке экстремума нет. Действительно,
. В этой точке экстремума нет. Действительно, 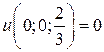 , а в сколь угодно малой окрестности точки
, а в сколь угодно малой окрестности точки 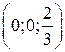 функция принимает как положительные, так и отрицательные значения. Например,
функция принимает как положительные, так и отрицательные значения. Например, 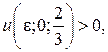 если
если 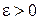 , и
, и 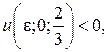 если
если 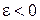 .
.
Пример 10.3. Найти экстремум функции 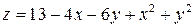 при условии
при условии 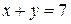 методом множителей Лагранжа.
методом множителей Лагранжа.
Решение. Составим функцию Лагранжа:
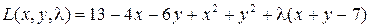 ,
,
где λ – множители Лагранжа.
Исследуем функцию 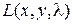 на экстремум. Определим стационарные точки, используя необходимые условия существования экстремума. Найдем частные производные функции и приравняем их к нулю:
на экстремум. Определим стационарные точки, используя необходимые условия существования экстремума. Найдем частные производные функции и приравняем их к нулю:
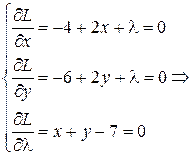
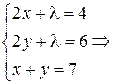
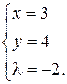
Следовательно, имеется одна стационарная точка 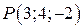 . Проверим, является ли эта точка точкой экстремума. Вычислим второй дифференциал функции
. Проверим, является ли эта точка точкой экстремума. Вычислим второй дифференциал функции 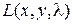 . Для этого необходимо найти частные производные второго порядка в точке
. Для этого необходимо найти частные производные второго порядка в точке 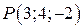 :
:
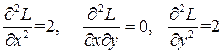 .
.
Тогда дифференциал второго порядка можно записать следующим образом:
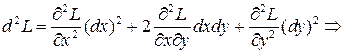
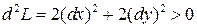 .
.
Так как 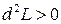 , то в точке
, то в точке 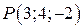 функция имеет условный ми-
функция имеет условный ми-
нимум:
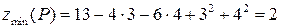 .
.
Пример 10.4. Найти условные экстремумы функции
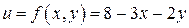
относительно уравнения связи
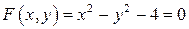 .
.
Решение. Функции 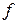 и
и 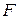 непрерывно дважды дифференцируемы. Матрица Якоби в данном случае имеет вид
непрерывно дважды дифференцируемы. Матрица Якоби в данном случае имеет вид 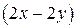 , и ее ранг равен единице во всех точках, удовлетворяющих уравнению связи. Следовательно, можно применить метод Лагранжа. Запишем функцию Лагранжа:
, и ее ранг равен единице во всех точках, удовлетворяющих уравнению связи. Следовательно, можно применить метод Лагранжа. Запишем функцию Лагранжа:
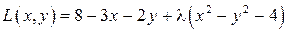 .
.
Согласно необходимым условиям получаем систему
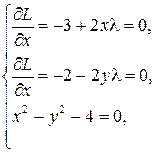
из которой находим, что 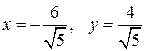 при
при 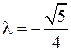 и
и
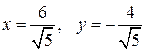 при
при 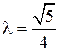 . Таким образом, функция
. Таким образом, функция 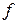 может иметь условный экстремум только в двух точках:
может иметь условный экстремум только в двух точках: 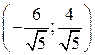 и
и 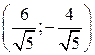 .
.
Вычислим второй дифференциал функции Лагранжа. Так как
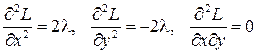 , то
, то 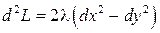 .
.
Найдем первый дифференциал функции 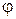 :
: 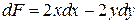 .
.
В точках 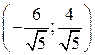 и
и 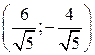 дифференциалы
дифференциалы 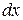 и
и 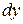 связаны равенством
связаны равенством 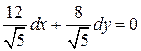 . Откуда
. Откуда 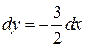 . Следовательно,
. Следовательно, 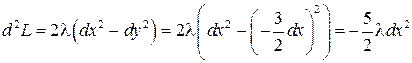 . Тогда второй дифференциал функции Лагранжа в точке
. Тогда второй дифференциал функции Лагранжа в точке 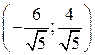 является положительно определенной квадратичной формой
является положительно определенной квадратичной формой
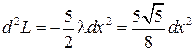 ,
,
а в точке 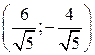 – отрицательно определенной квадратичной формой
– отрицательно определенной квадратичной формой
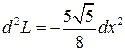 .
.
Следовательно, функция 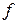 в точке
в точке 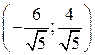 имеет условный минимум
имеет условный минимум 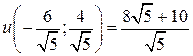 , а в точке
, а в точке 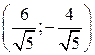 – условный максимум
– условный максимум 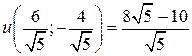 .
.
Пример 10.5. Найти наименьшее и наибольшее значения функции 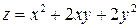 в замкнутой области
в замкнутой области 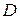 , заданной системой неравенств
, заданной системой неравенств 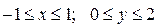 .
.
Решение. Определим стационарные точки заданной функции в данной области 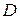 и изучим поведение функции на границе области. Найдем частные производные первого и второго порядка функции
и изучим поведение функции на границе области. Найдем частные производные первого и второго порядка функции 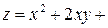
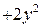 :
:
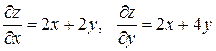 ;
;
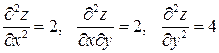 .
.
Из системы уравнений (необходимое условие существования экстремума) определим стационарную точку:
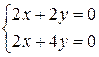
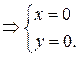
Стационарная точка 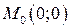 принадлежит области и является точкой экстремума (достаточное условие), т. к.
принадлежит области и является точкой экстремума (достаточное условие), т. к.
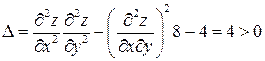 .
.
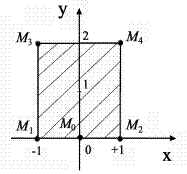 Рис. 12 Рис. 12 | Точка 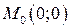 является точкой минимума, поскольку является точкой минимума, поскольку 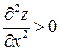 и и 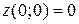 . Исследуем поведение функции на границе области. На оси Ox . Исследуем поведение функции на границе области. На оси Ox 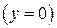 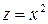 и наибольшие значения функция принимает в наиболее удалённых от нуля точках, т. е. при и наибольшие значения функция принимает в наиболее удалённых от нуля точках, т. е. при 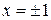 . Это точки . Это точки 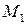 и и 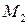 (рис. 19). (рис. 19). |
На прямой 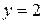
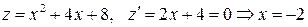 .
.
Точка 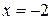 – точка минимума
– точка минимума 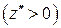 . Для всех
. Для всех 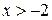 функция возрастает, поэтому в пределах области наибольшее значение она принимает в точке
функция возрастает, поэтому в пределах области наибольшее значение она принимает в точке 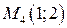 .
.
На прямой 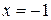
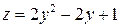 ;
; 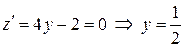 .
.
Точка 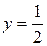 – точка минимума, В пределах области наибольшего значения функция достигает в точке
– точка минимума, В пределах области наибольшего значения функция достигает в точке 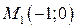 или в точке
или в точке 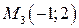 .
.
На прямой 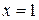
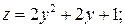
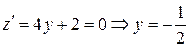 .
.
Точка 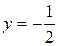 – точка минимума. В пределах области наибольшее значение функция принимает в точке
– точка минимума. В пределах области наибольшее значение функция принимает в точке 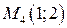 .
.
Осталось вычислить значения функции в точках 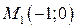 ,
, 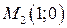 ,
, 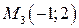 ,
, 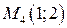 ; значение в точке
; значение в точке 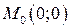 вычислено выше
вычислено выше 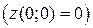 :
:
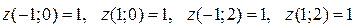 .
.
Таким образом, сравнивая все полученные значения функции, выбираем из них наибольшее (в точке 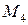 ) и наименьшее (в точке
) и наименьшее (в точке  ) значения:
) значения:
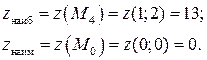
Пример 10.6. Найти наименьшее и наибольшее значения функции 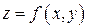 в замкнутой области D, заданной системой неравенств
в замкнутой области D, заданной системой неравенств
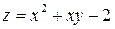 ,
, 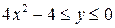 .
.
Решение. Область ограничена прямой 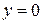 и параболой
и параболой 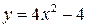 . Вначале исследуем функцию на экстремум: найдем частные производные и приравняем их к нулю. Определим стационарные точки:
. Вначале исследуем функцию на экстремум: найдем частные производные и приравняем их к нулю. Определим стационарные точки:
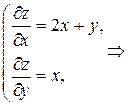
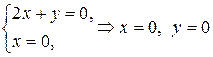 .
.
Стационарная точка: 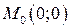 . Используем достаточные условия экстремума:
. Используем достаточные условия экстремума:
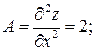
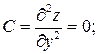
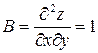 .
.
Так как 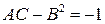 , функция экстремума не имеет. Поэтому она принимает наибольшее и наименьшее значения на границах заданной области.
, функция экстремума не имеет. Поэтому она принимает наибольшее и наименьшее значения на границах заданной области.
Исследуем поведение функции на границах области.
1. Если 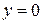 ,
, 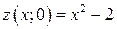 ,
, 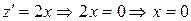 ,
, 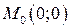 – точка минимума, т. к.
– точка минимума, т. к. 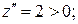
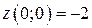 .
.
2. Если 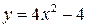 , то
, то
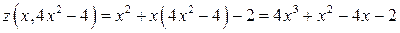 ;
; 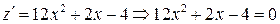 .
.
Имеем две критические точки:
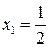 и
и 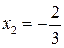 ;
; 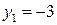 ,
, 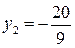 ;
; 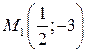 ,
, 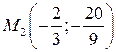 .
.
По второму достаточному условию 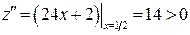 , значит, M 1 – точка минимума. Поскольку
, значит, M 1 – точка минимума. Поскольку 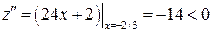 , то M 2 – точка максимума. Вычисляем значения функций в этих точках:
, то M 2 – точка максимума. Вычисляем значения функций в этих точках:
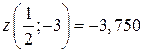 ;
; 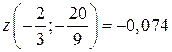 .
.
3. Вычисляем значения функции в граничных точках 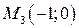 и
и 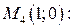
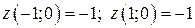 .
.
Выберем наибольшее и наименьшее значение из найденных значений:
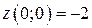 ;
; 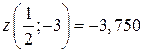 ;
; 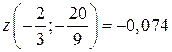 ;
;
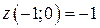 ;
; 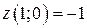 .
.
Таким образом, наибольшее значение и наименьшее значение функции в заданной области составляют
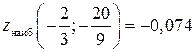 ;
; 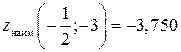 .
.
Исследовать на экстремум следующие функции нескольких переменных:
10.1. 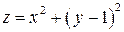 . . | 10.2. 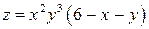 . . |
10.3. 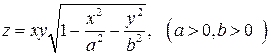 .
.
10.4. 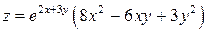 . . | 10.5. 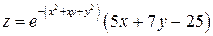 . . |
10.6. 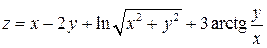 .
.
10.7. 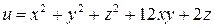 .
.
10.8. 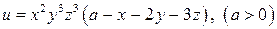 .
.
10.9. 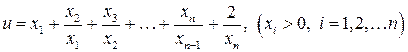 .
.
10.10. Доказать, что функция 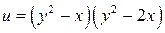 :
:
1) вдоль каждой прямой, проходящей через точку 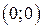 , имеет в этой точке минимум;
, имеет в этой точке минимум;
2) не имеет минимума в точке 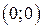 .
.
Найти экстремальные значения заданной неявно функции:
10.11. 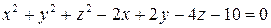 . . | |
10.12. 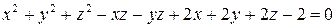 . . | |
10.13. 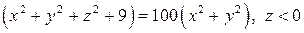 . . |
Найти точки условного экстремума следующих функций:
10.14. 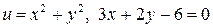 . . | 10.15. 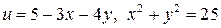 . . | |
10.16. 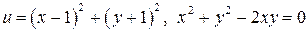 . . | ||
10.17. 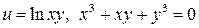 . . | 10.18. 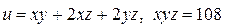 . . | |
10.19. 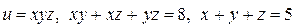 . . | ||
10.20. 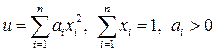 . . | ||
Найти наибольшее 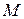 и наименьшее
и наименьшее 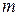 значения функции на заданном множестве:
значения функции на заданном множестве:
10.21. 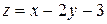 , если , если 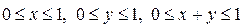 . . | |
10.22. 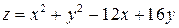 , если , если 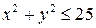 . . | |
10.23. 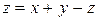 , если , если 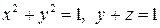 . . |
10.24. Показать, что функция 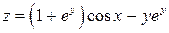 имеет бесконечное множество максимумов и ни одного минимума.
имеет бесконечное множество максимумов и ни одного минимума.
10.25. Найти расстояние между поверхностями
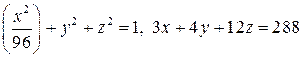 .
.
Ответы: 10.1. 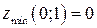 . 10.2.
. 10.2. 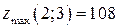 , нестрогий минимум
, нестрогий минимум 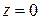 при
при 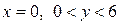 , нестрогий максимум
, нестрогий максимум 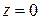 при
при 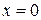 ,
, 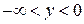 ,
, 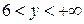 . 10.3.
. 10.3. 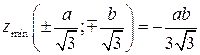 ,
, 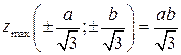 .
.
10.4. 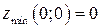 , седло
, седло 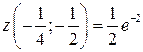 .
.
10.5. 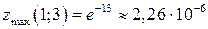 ,
, 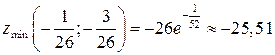 .
.
10.6. Седло 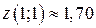 . 10.7.
. 10.7. 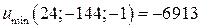 .
.
10.8. 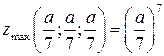 .
.
10.9. 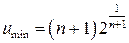 при
при 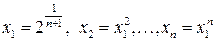 .
.
10.11. 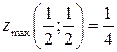 .
.
10.12. 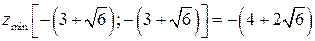 ;
; 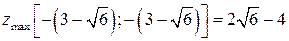 .
.
10.13. Нестрогий минимум 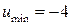 в точках окружности,
в точках окружности, 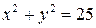 .
.
10.14. 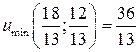 .
.
10.15. 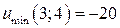 ,
, 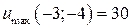 . 10.16.
. 10.16. 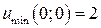 .
.
10.17. 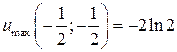 . 10.18.
. 10.18. 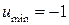 ,
, 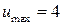 .
.
10.19. 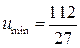 ,
, 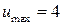 .
.
10.20. 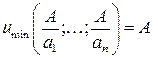 , где
, где 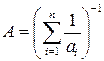 . 10.21.
. 10.21. 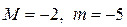 .
.
10.22. 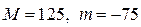 .
.
10.23. 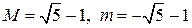 . 10.25.
. 10.25. 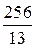 .
.
 2015-03-27
2015-03-27 11509
11509