2015-03-07
903
(формула парабол или квадратурная формула)
Разделим отрезок интегрирования [ a, b ] на четное число отрезков п =2 m. Площадь криволинейной трапеции, ограниченной графиком функции f (x) заменим на площадь криволинейной трапеции, ограниченной параболой второй степени с осью симметрии, параллельной оси Оу и проходящей через точки кривой, со значениями f (x 0 ), f (x 1 ), f (x 2 ).
Для каждой пары отрезков построим такую параболу (рис. 8.4.1).
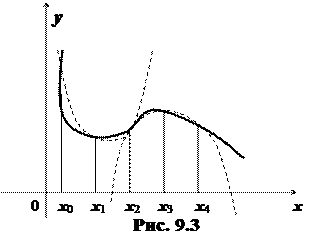Уравнения этих парабол имеют вид Ax 2 + Bx + C, где коэффициенты А, В, С могут быть легко найдены по трем точкам пересечения параболы с исходной кривой.
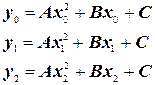(9.4)
Обозначим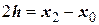 
.
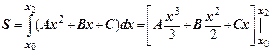
Если принять х 0 = – h, x 1 = 0, x 2 = h, то
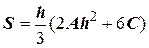(9.5)
Тогда уравнения значений функции (9.4) имеют вид:
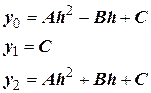
C учетом этого: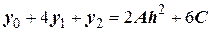 
.
Отсюда уравнение (8.5.1) примет вид: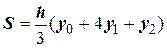 
Тогда
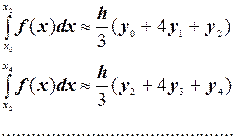
Складывая эти выражения, получаем формулу Симпсона:
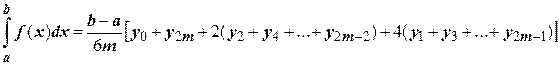
Чем больше взять число m, тем более точное значение интеграла будет получено.
