Метод вариации произвольной постоянной

Найдем сначала общее решение соответствующего ЛОДУ 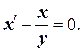Разделяя переменные и интегрируя, получим ln | x | = ln | y | + ln | C ₁|, C ₁ .

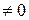Общее решение ЛОДУ можно записать так х= Су, 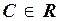(так как х= 0 – решение).

Общее решение заданного (преобразованного) уравнения ищем в виде х=С (у) у (постоянную С заменили неизвестной функцией С (у)). Подставляя х и 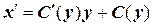в ЛНДУ, придем к равенству:

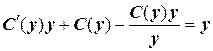, т.е.

.

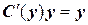Отсюда 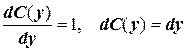. Интегрируя, имеем С (у) = у + С.

Таким образом, общее решение ЛНДУ есть х = (у + С) у или х = у ² + Су. Заметим, что у = 0 также является решением, и для нашего примера оно является особым.