II. Метод Бернулли

Пусть 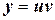. Тогда 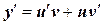и уравнение принимает вид

,

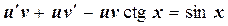или

.

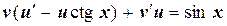Подберем функцию u (x) так, чтобы выражение в скобках равнялось нулю, т.е. решим первое дифференциальное уравнение с разделяющимися переменными ,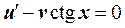

.

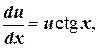
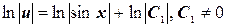Откуда u=С ₁ × sin x.

Пусть С ₁=1, u= sin x.

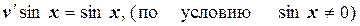, отсюда 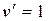, т.е. .

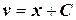Итак, y= (x+C)· sin x, 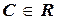есть общее решение данного ЛНДУ.

№9. Найти общее решение уравнения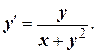

Решение. Данное уравнение не является линейным относительно х и 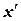. Так как 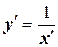, то приведем исходное уравнение к виду (10.6):

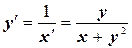, т.е. 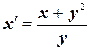или 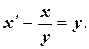Далее это ДУ решим двумя методами: