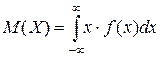Плотностью вероятности, или плотностью распределения f(x) непрерывной случайной величины Х, называется производная её функции распределения:
f(x) = F' (x).
Ее также называют дифференциальной функцией распределения.
График плотности распределения f(x) называется кривой распределения.
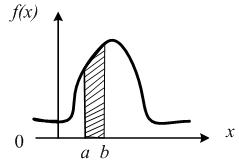
Рис. 12.4. Плотность распределения
Свойства плотности вероятности:
1.f(х) 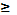 0 (свойство неотрицательности).
0 (свойство неотрицательности).
2. Площадь фигуры, ограниченной кривой распределения и осью абсцисс, равна единице (свойство нормированности).
3. Вероятность попадания непрерывной случайной величины в интервал [ а, b ] равна определенному интегралу от ее плотности вероятности в пределах от а до b.
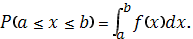
Полученная вероятность равна площади фигуры, ограниченной сверху кривой распределения и опирающейся на отрезок [ а, b ].
Непрерывная случайная величина описывается следующими числовыми характеристиками:
2. Дисперсия: 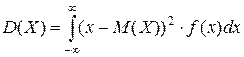 или
или 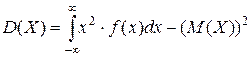
Найдите математическое ожидание и дисперсию случайной величины X, если плотность распределения:
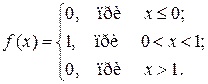
Решение:
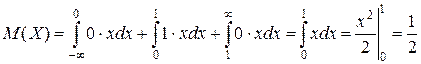 .
.
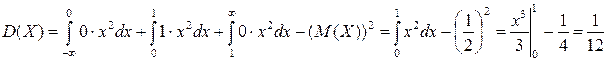 .
.
 2015-03-07
2015-03-07 1279
1279