Математическая статистика – это раздел математики, изучающий приближенные методы сбора и анализа данных по результатам эксперимента для выявления существующих закономерностей, т.е. отыскания законов распределения случайных величин и их числовых характеристик.
В математической статистике принято выделять два основных направления исследований:
1. Оценка параметров генеральной совокупности.
2. Проверка статистических гипотез (некоторых априорных предположений).
Основными понятиями математической статистики являются: генеральная совокупность, выборка, теоретическая функция распределения.
Генеральной совокупностью является набор всех мыслимых статистических данных при наблюдениях случайной величины.
ХГ = {х1, х2, х3, …, хN, } = { хi ; i=1,N }
Наблюдаемая случайная величина Х называется признаком или фактором выборки. Генеральная совокупность – есть статистический аналог случайной величины, ее объем N обычно велик, поэтому из нее выбирается часть данных, называемая выборочной совокупностью или просто выборкой.
ХВ = {х1, х2, х3, …, хn, } = { хi ; i=1,n }
ХВ Ì ХГ, n £ N
Выборка – это совокупность случайно отобранных наблюдений (объектов) из генеральной совокупности для непосредственного изучения. Количество объектов в выборке называется объемом выборки и обозначается n. Обычно выборка составляет 5%-10% от генеральной совокупности.
Использование выборки для построения закономерностей, которым подчинена наблюдаемая случайная величина, позволяет избежать ее сплошного (массового) наблюдения, что часто бывает ресурсоемким процессом, а то и просто невозможным.
Например, популяция представляет собой множество индивидуумов. Изучение целой популяции трудоемко и дорого, поэтому собирают данные по выборке индивидуумов, которых считают представителями этой популяции, позволяющими сделать вывод относительно этой популяции.
Однако, выборка обязательно должна удовлетворять условию репрезентативности, т.е. давать обоснованное представление о генеральной совокупности. Как сформировать репрезентативную (представительную) выборку? В идеале стремятся получить случайную (рандомизированную) выборку. Для этого составляют список всех индивидуумов в популяции и случайно их отбирают. Но иной раз затраты при составлении списка могут оказаться недопустимыми и тогда берут приемлемую выборку, например, одну клинику, больницу и исследуют всех пациентов в этой клинике с данным заболеванием.
Каждый элемент выборки 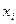 называется вариантой. Число повторений варианты
называется вариантой. Число повторений варианты 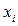 в выборке называется частотой встречаемости
в выборке называется частотой встречаемости 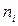 . Величина
. Величина 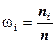 называется относительной частотой варианты, т.е. находится как отношение абсолютной частоты варианты
называется относительной частотой варианты, т.е. находится как отношение абсолютной частоты варианты 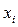 ко всему объему выборки. Последовательность вариант, записанных в возрастающем порядке, называется вариационным рядом.
ко всему объему выборки. Последовательность вариант, записанных в возрастающем порядке, называется вариационным рядом.
Рассмотрим три формы вариационного ряда: ранжированный, дискретный и интервальный.
Ранжированный ряд - это перечень отдельных единиц совокупности в порядке возрастания изучаемого признака.
Дискретный вариационный ряд представляет собой таблицу, состоящую из граф, либо строк: конкретного значения признака хi и абсолютной частоты ni (или относительной частоты ωi) проявления i-го значения признака x.
Примером вариационного ряда служит таблица
| Значение | 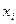 | 14,3 | 14,7 | 15,0 | 15,5 | |
| Частота | 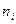 | 0,08 | 0,16 | 0,29 | 0,34 | 0,13 |
Статистическое распределение – это совокупность вариант 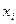 и соответствующих им частот
и соответствующих им частот 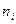 . Для проверки правильности записи статистического распределения используют условие нормировки:
. Для проверки правильности записи статистического распределения используют условие нормировки: 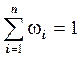 .
.
Задано распределение частот выборки объема n=20.
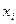 | |||
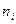 |
Написать распределение относительных частот.
Решение: Найдем относительные частоты. Для этого разделим частоты на объем выборки:
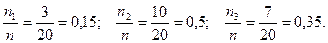
Распределение относительных частот имеет вид:
 | |||
 | 0,15 | 0,5 | 0,35 |
Контроль: 0,15 + 0,5 + 0,35 = 1.
Дискретный ряд можно изобразить графически. В прямоугольной декартовой системе координат отмечаются точки с координатами (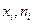 ) или (
) или (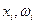 ), которые соединяются прямыми линиями. Такую ломаную называют полигоном частот.
), которые соединяются прямыми линиями. Такую ломаную называют полигоном частот.
Построить дискретный вариационный ряд (ДВР) и начертить полигон распределения 45 абитуриентов по числу баллов, полученных ими на приемных экзаменах:
39 41 40 42 41 40 42 44 40 43 42 41 43 39 42 41 42 39 41 37 43 41 38 43 42 41 40 41 38 44 40 39 41 40 42 40 41 42 40 43 38 39 41 41 42.
Решение: Для построения вариационного ряда различные значения признака x (варианты) располагаем в порядке их возрастания и под каждым из этих значений записываем его частоту.
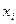 | ||||||||
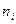 |
Построим полигон этого распределения:
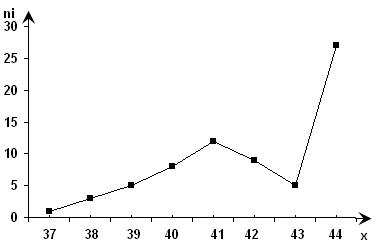
Рис. 13.1. Полигон частот
Интервальный вариационный ряд используется при большом числе наблюдений. Для построения такого ряда надо выбрать число интервалов признака и установить длину интервала. При большом числе групп величина интервала будет минимальна. Число групп в вариационном ряду можно найти по формуле Стерджеса: 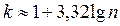 (k-число групп, n - объем выборки), а ширину интервала –
(k-число групп, n - объем выборки), а ширину интервала – 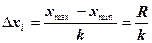
где 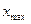 - максимальное;
- максимальное; 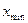 - минимальное значения вариант, а их разность R носит название размаха вариации.
- минимальное значения вариант, а их разность R носит название размаха вариации.
Исследуется выборка из 100 человек из совокупности всех студентов медицинского ВУЗа.
Решение: Рассчитаем число групп: 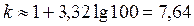 . Таким образом, для составления интервального ряда данную выборку лучше разбить на 7 или 8 групп. Совокупность групп, на которые разбиваются результаты наблюдений и частот получения результатов наблюдений в каждой группе, называют статистической совокупностью.
. Таким образом, для составления интервального ряда данную выборку лучше разбить на 7 или 8 групп. Совокупность групп, на которые разбиваются результаты наблюдений и частот получения результатов наблюдений в каждой группе, называют статистической совокупностью.
Для наглядного представления статистического распределения пользуются гистограммой.
Гистограмма частот – это ступенчатая фигура, состоящая из смежных прямоугольников, построенных на одной прямой, основания которых одинаковы и равны ширине интервала, а высота равна или частоте попадания в интервал 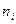 или относительной частоте ωi.
или относительной частоте ωi.
Наблюдения за числом частиц, попавших в счетчик Гейгера, в течение минуты дали следующие результаты:
21 30 39 31 42 34 36 30 28 30 33 24 31 40 31 33 31 27 31 45 31 34 27 30 48 30 28 30 33 46 43 30 33 28 31 27 31 36 51 34 31 36 34 37 28 30 39 31 42 37.
Построить по этим данным интервальный вариационный ряд с равными интервалами (I интервал 20-24; II интервал 24-28 и т.д.) и начертить гистограмму.
Решение: n = 50
| Интервал | 20-24 | 24-28 | 28-32 | 32-36 | 36-40 | 40-44 | 44-48 | 48-52 |
Частота 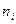 |
Гистограмма этого распределения имеет вид:
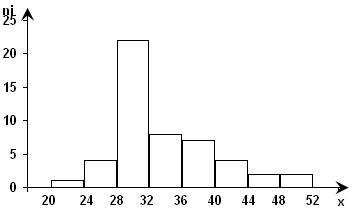
Рис. 13.2. Гистограмма распределения
Варианты заданий
№ 13.1. Через каждый час измерялось напряжение тока в электросети. При этом были получены следующие значения (В):
227 219 215 230 232 223 220 222 218 219 222 221 227 226 226 209 211 215 218 220 216 220 220 221 225 224 212 217 219 220.
Построить статистическое распределение и начертить полигон.
№ 13.2. Наблюдения за сахаром крови у 50 человек дали такие результаты:
3.94 3.84 3.86 4.06 3.67 3.97 3.76 3.61 3.96 4.04
3.82 3.94 3.98 3.57 3.87 4.07 3.99 3.69 3.76 3.71
3.81 3.71 4.16 3.76 4.00 3.46 4.08 3.88 4.01 3.93
3.92 3.89 4.02 4.17 3.72 4.09 3.78 4.02 3.73 3.52
3.91 3.62 4.18 4.26 4.03 4.14 3.72 4.33 3.82 4.03
Построить по этим данным интервальный вариационный ряд с равными интервалами (I - 3.45-3.55; II - 3.55-3.65 и т. д.) и изобразить его графически, начертить гистограмму.
№ 13.3. Построить полигон частот распределения скорости оседания эритроцитов (СОЭ) у 100 человек:
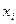 | |||||
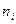 |
№ 13.4. Построить гистограмму распределения скорости оседания эритроцитов (СОЭ) у 50 человек:
| Интервал | 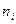 |
| 2-5 | |
| 5-8 | |
| 8-11 | |
| 11-14 |
 2015-03-07
2015-03-07 43548
43548








