Метод контурных токов

При расчете методом контурных токов полагают, что в каждом независимом контуре схемы течет свой контурный ток. Уравнения составляют относительно контурных токов, после чего через них определяют токи ветвей.
Таким образом, метод контурных токов можно определить как метод расчета, в котором за искомые принимают контурные токи. Число неизвестных в этом методе равно числу уравнений, которые необходимо было бы составить для схемы по второму закону Кирхгофа.
Следовательно, метод контурных токов более экономен при вычислительной работе, чем метод на основе законов Кирхгофа (в нем меньше число уравнений).
Вывод основных расчетных уравнений приведем применительно к схеме рис. 2.12, в которой два независимых контура. Положим, что в левом контуре по часовой стрелке течет контурный ток I₁₁ а в правой (также по часовой стрелке) — контурный ток I₂₂. Для каждого контура составим уравнения по второму закону Кирхгофа. При этом учтем, что по смежной ветви (с сопротивлением R5) течет сверху вниз ток I₁₁. — I₂₂ Направления обхода контуров примем также по часовой стрелке.

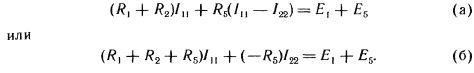Для второго контура

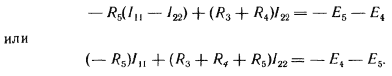В уравнении (б) множитель при токе I₁₁, являющийся суммой сопротивлений первого контура, обозначим через R₁₁, множитель при токе I₂₂ (сопротивление смежной ветви, взятое со знаком минус) — через R₁₂.
Перепишем эти уравнения следующим образом:

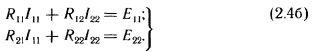Здесь

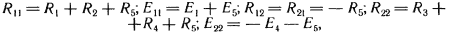где R₁₁ — полное или собственное сопротивление первого контура; R₁₂ — сопротивление смежной ветви между первым и вторым контурами, взятое со знаком минус; E₁₁ — контурная ЭДС первого контура, равная алгебраической сумме ЭДС этого контура (в нее со знаком плюс входят те ЭДС, направления которых совпадают с направлением обхода контура); R₂₂ — полное или собственное сопротивление второго контура; R₂₁ — сопротивление смежной ветви у между первым и вторым контурами, взятое со знаком минус; E₂₂ — контурная ЭДС второго контура.
В общем случае можно сказать, что сопротивление смежной ветви между K- и T-контурами (R_km) входит в уравнение со знаком минус, если направления контурных токов I_kk и I_TT вдоль этой ветви встречны, и со знаком плюс, если направления этих токов согласны.
Если в схеме больше двух контуров, например три, то система уравнений выглядит следующим образом:

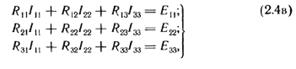или в матричной форме

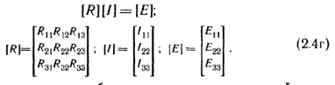Рекомендуется для единообразия в знаках сопротивлений с разными индексами все контурные токи направлять в одну и ту же сторону, например по часовой стрелке.
В результате решения системы уравнений какой-либо один или несколько контурных токов могут оказаться отрицательными.
В ветвях, не являющихся смежными между соседними контурами (например, в ветви с сопротивлениями R₁, R₂ рис. 2.12), найденный контурный ток является действительным током ветви. В смежных ветвях через контурные токи определяют токи ветвей. Например, в ветви с сопротивлением R₅ протекающий сверху вниз ток равен разности Ш₁₁ — R₂₂.
Если в электрической цепи имеется п независимых контуров, то число уравнений тоже равно n.
Общее решение системы n уравнений оносительно тока I_KK:

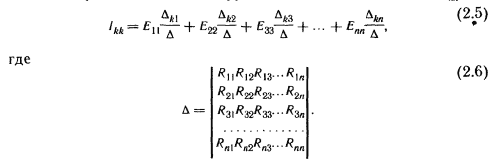— определитель системы.
Алгебраическое дополнение Δ_km получено из определителя Δ путем вычеркивания K-го столбца и m -й строки и умножения полученного определителя на (—1)^{k + m}.
Если из левого верхнего угла определителя провести диагональ в его правый нижний угол (главная диагональ) и учесть, что R_km = R_kmk, то можно убедиться в том, что определитель делится на две части, являющиеся зеркальным отображением одна другой. Это свойство определителя называют симметрией относительно главной диагонали. В силу симметрии определителя относительно главной диагонали Δ_km = Δ_mk
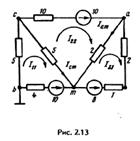
Пример 13. Найти токи в схеме (рис. 2.13) методом контурных токов. Числовые значения сопротивлений в омах и ЭДС в вольтах указаны на рисунке.
Решение. Выберем направления всех контурных токов I₁₁, I₂₂ и I₃₃ по часовой стрелке. Определяем: R₁₁ = 5 + 5 + 4 = 14 Ом; R₂₂ = 5 + 10 + 2 = 17 Ом; R₃₃ = 2+ + 2+ 1 =5 Ом; К₁₂ = К₂₁ = — 5 Ом; R₁₃ = R₃₁ = 0; R₂₃ = R₃₂ = - 2 Ом; E₁₁ = -10 В; E₃₃ = -8.

Записываем систему уравнений:

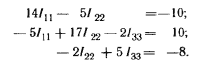определитель системы

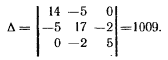подсчитаем контурные токи

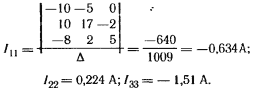Ток в ветви cm I_cm = I₁₁ - I₂₂ = -0,634-0,224=-0,86 A. Ток в ветви am I_am = I₂₂ - I₃₃ = 0,224 + 1,51 = 1,734 A.
Формула (2.5) в ряде параграфов используется в качестве исходной при рассмотрении таких важных вопросов теории линейных электрических цепей, как определение входных и взаимных проводимостей ветвей, принцип взаимности, метод наложения и линейные соотношения в электрических цепях.
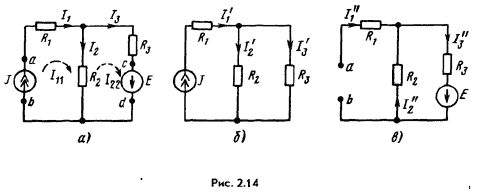
Составлению уравнений по методу контурных токов для схем с источниками тока присущи некоторые особенности. В этом случае полагаем, что каждая ветвь с источником тока входит в контур, замыкающийся через ветви с источниками ЭДС и сопротивлениями, и что токи в этих контурах известны и равны токам соответствующих источников тока. Уравнения составляют лишь для контуров с неизвестными контурными токами. Если для схемы рис. 2.14, а принять, что контурный ток I₁₁ = J течет согласно направлению часовой стрелки по первой и второй ветвям, а контурный ток I₂₂= I₃ замыкается также по часовой стрелке по второй и третьей ветвям, то, согласно методу контурных токов, получим только одно уравнение с неизвестным током I₂₂: (R₂ + R₃)I₂₂ - R₂I = E.
Отсюда I₂₂ = 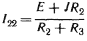и ток второй ветви I₂ = I ₁₁ - I ₂₂/