Обозначим число таких молекул 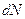 . Тогда
. Тогда
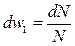 ,
,
где 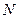 – число молекул в этом объеме.
– число молекул в этом объеме.
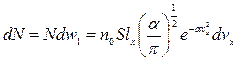 ,
,
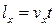 .
.
Давление, которые создают эти молекул
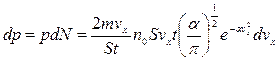 .
.
За этот же промежуток времени 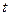 о грань
о грань 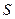 ударяют молекулы и с другими скоростями. Поэтому давление от всех молекул
ударяют молекулы и с другими скоростями. Поэтому давление от всех молекул
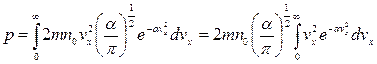 .
.
Для решения этого интеграла воспользуемся интегралом Пуассона
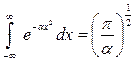 .
.
Это выражение можно рассмотреть как функцию 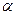 . Возьмем производную по этому параметру
. Возьмем производную по этому параметру
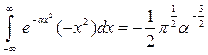 .
.
Учитывая, что подынтегральная функция четная, можно записать
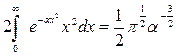 .
.
Тогда
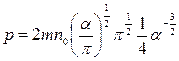 ,
,
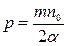 .
.
В курсе школьной и общей физики рассматривается самостоятельно молекулярно-кинетическая теория. В этой модели есть определение давления, температуры.
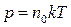 .
.
Приравняем полученное выражение для давления с выражением для давления в молекулярно-кинетической теории и выразим 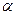
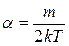 .
.
Параметр 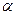 отражает свойства молекулы, а именно маску и свойства окружающей среды – температура.
отражает свойства молекулы, а именно маску и свойства окружающей среды – температура.
Таким образом, функция распределения Максвелла полностью определена.
Найти среднее значение 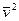 (квадрат модуля).
(квадрат модуля).
Для решения этой задачи необходимо знать функцию распределения по модулю скоростей. Для её решения целесообразно перейти в сферическую систему координат пространства скоростей.
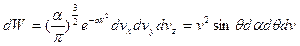
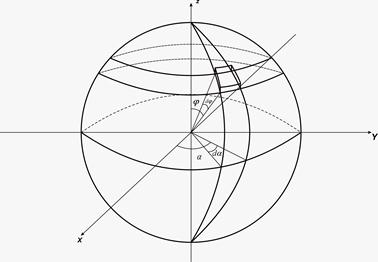
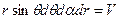
В пространстве v роль полярного радиуса выполняет модуль вектора v.
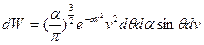 - проинтегрируем по
- проинтегрируем по 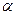
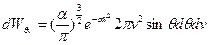
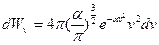
Полученное выражение 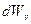 - вероятность того, что модуль скорости произвольно выбранной молекулы попадает в промежуток
- вероятность того, что модуль скорости произвольно выбранной молекулы попадает в промежуток 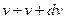 . Т.е. в тонкий шаровой слой толщиной
. Т.е. в тонкий шаровой слой толщиной 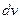 . Это и есть то, что мы искали.
. Это и есть то, что мы искали.
Искомая функция распределения по модулю v.
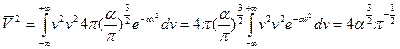

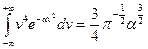
 2015-03-27
2015-03-27 315
315








