Статистическая физика.
Лекция №1.
Введение.
Одним из основных понятий статистической физики является понятие «идеального газа». В рамках классической модели под идеальным газом будем понимать газ из мельчайших частиц – молекул, которые находятся в состоянии прямолинейного равномерного движения. В идеальном газе взаимодействие между молекулами на расстоянии отсутствует.
Между молекулами возможны и происходят абсолютно упругие удары, при которых частицы обмениваются энергией (потерь энергии не происходит). В общем случае частицы находятся в состоянии хаотического движения, скорости частиц меняются непредсказуемым образом.
Объектом рассмотрения будет являться идеальный газ, находящийся в замкнутом объеме, при этом температура окружающей среды полагается неизменной (система находится в термостате). В такой системе распределение частиц по скоростям остается неизменным, хотя скорости отдельно взятых молекул меняются.
Нашей задачей является получение аналитического выражения этой зависимости.
Максвелловское распределение молекул по скоростям в идеальном газе.
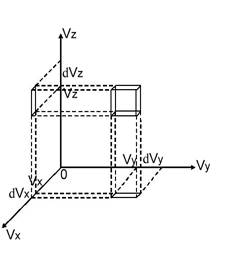
Введем декартово пространство скоростей. Выделим некоторый интервал скоростей 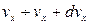 .
.
Какова вероятность того, что произвольно выбранная молекула будет иметь проекцию скорости, попадающую в этот интервал? Обозначим эту вероятность 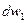 ,введем функцию
,введем функцию 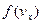 . Тогда вероятность будет зависеть от:
. Тогда вероятность будет зависеть от:
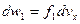 . (*)
. (*)
Рассуждая аналогичным образом для других проекций:
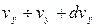 :
: 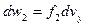 ;
;
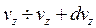 :
: 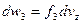 .
.
Выделим на рисунке соответствующую область. Запишем выражение 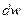 того события, сто произвольно выбранная молекула попадает в объем
того события, сто произвольно выбранная молекула попадает в объем
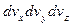 :
: 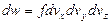 .
.
Учитывая, что значения проекций скоростей молекул друг от друга не зависят, то вероятность того, что значения проекций в некоторый момент времени попадают в указанные интервалы, можно записать:
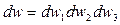 - согласно закону теории вероятности, как 3 независимых друг от друга события.
- согласно закону теории вероятности, как 3 независимых друг от друга события.
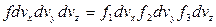
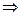
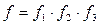 .
.
С другой стороны: 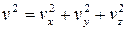 .
.
Предположим: 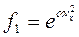 .
.
Тогда оба требования удовлетворяются:
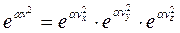
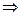
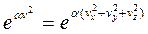 .
.
Выражение 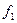 через экспоненту противоречит смыслу выражения (*), т. к. с ростом скорости возрастает и вероятность
через экспоненту противоречит смыслу выражения (*), т. к. с ростом скорости возрастает и вероятность 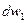 , что в действительности не так.
, что в действительности не так.
Установить данное противоречие можно, поставив знак «-»: 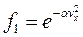 .
.
Тогда с возрастанием скорости вероятность будет уменьшаться.
В математике известен 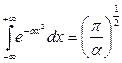 - интеграл Пуассона.
- интеграл Пуассона.
Проинтегрируем выражение (*):
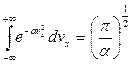 .
.
Данный интеграл отражает вероятность того события, что значение 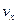 у произвольно выбранной молекулы будет находиться в пределах
у произвольно выбранной молекулы будет находиться в пределах 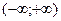 . Очевидно, что вероятность этого события равна 1. поэтому разделим обе части этого равенства на правую часть:
. Очевидно, что вероятность этого события равна 1. поэтому разделим обе части этого равенства на правую часть:
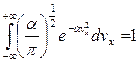 ,
,
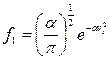 .
.
Аналогичные рассуждения справедливы для двух других проекций.
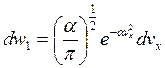 ;
;
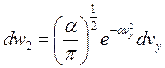 ;
;
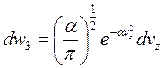 ;
;
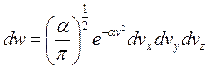 .
.
Где 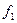 - функция распределения.
- функция распределения.
Для выяснения вида параметра 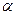 проведем следующие рассуждения: сделаем рисунок объема, в котором находится газ. Выделим некоторую молекулу, у которой проекция скорости
проведем следующие рассуждения: сделаем рисунок объема, в котором находится газ. Выделим некоторую молекулу, у которой проекция скорости 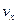 , находящаяся недалеко от боковой грани
, находящаяся недалеко от боковой грани 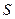 .
.
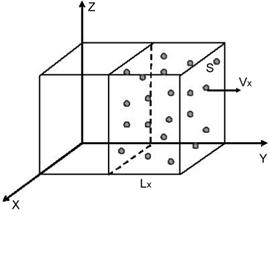
Предположим, что на своем пути молекула не испытывает соударений. Т. к. удар абсолютно упругий, то изменение импульса у частицы после удара будет 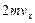 .
.
Из школьного курса (II закон Ньютона): 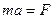 ,
,
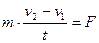 ;
;
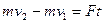 ;
;
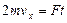 .
.
Где 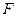 - сила, с которой молекула действует на стенку,
- сила, с которой молекула действует на стенку, 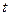 - время.
- время.
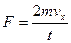 ;
;
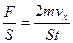
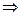
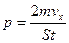 .
.
Моменту времени 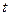 можно поставить в соответствие некоторое расстояние
можно поставить в соответствие некоторое расстояние 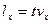 . Условно выделим на рисунке соответствующее расстояние
. Условно выделим на рисунке соответствующее расстояние 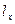 и объем. В выделенном объеме кроме выбранной нами молекулы существует еще много других молекул, проекция скорости которых
и объем. В выделенном объеме кроме выбранной нами молекулы существует еще много других молекул, проекция скорости которых 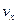 .
.
 2015-03-27
2015-03-27 538
538







