По-прежнему будем рассматривать сосуд с идеальным газом. Выделим в этом сосуде пространственный объём
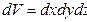 ,
,
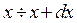 ,
,
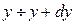 ,
,
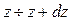 .
.
В пространстве скоростей выберем некоторый объем 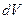 , который характеризуется
, который характеризуется
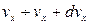 ,
,
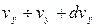 ,
,
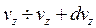 .
.
Вероятность того, что произвольно выбранная молекула попадет в этот интервал:
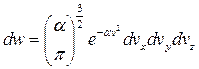
Сделаем переход от пространства скоростей к пространству импульсов:
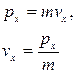 .
.
Тогда:
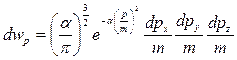 .
.
В пространственном объеме выделим элементарный объем.
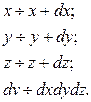
Вероятность того, что произвольно выбранная молекула имеет такие координаты:
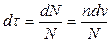 ,
,
где 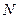 - общее число молекул в сосуде.
- общее число молекул в сосуде.
Допустим, что в некоторой бесконечно малой области объема известна концентрация 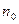 , потенциальная энергия молекул в этой области. Тогда с помощью закона распределения Больцмана:
, потенциальная энергия молекул в этой области. Тогда с помощью закона распределения Больцмана:
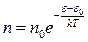 ,
,
где 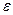 - потенциальная энергия в выделенном объеме.
- потенциальная энергия в выделенном объеме.
Вероятность того, что произвольно выбранная молекула одновременно принадлежит интервалу импульсов и интервалу координат (эти два события не зависят друг от друга):
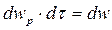 .
.
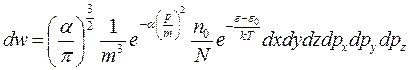 ;
;
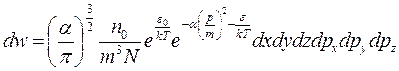 ;
;
Т. к. 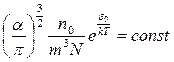 , обозначим через
, обозначим через 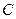 :
:
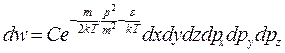 ;
;
Т. к. 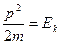 :
:
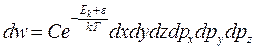 .
.
Произведение 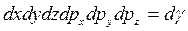 формально можно воспринимать как элемент объема в шестимерном пространстве.
формально можно воспринимать как элемент объема в шестимерном пространстве.
Число молекул в сосуде 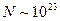 частиц, в результате получается огромное число элементарных объемчиков.
частиц, в результате получается огромное число элементарных объемчиков.
Присвоим каждому объемчику номер, так же присвоим номера молекулам.
В рамках классической физики это допускается, т. е. две молекулы различны.
Вероятность 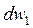 что молекула с номером 1 попадет в объемчик с тем же номером 1:
что молекула с номером 1 попадет в объемчик с тем же номером 1:
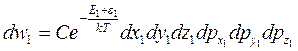 .
.
Вероятность события, что одновременно все молекулы попадут в объемы с такими же номерами что и у молекул:
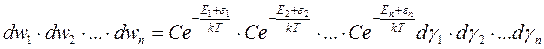 .
.
Обозначим вероятность этого события через 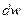 :
:
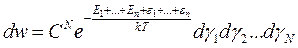 ,
,
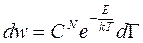 ,
,
где 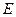 - полная энергия,
- полная энергия, 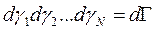 - элемент
- элемент 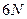 -мерного пространства,
-мерного пространства, 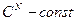 , можно всегда представить в виде
, можно всегда представить в виде 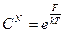 ,
, 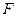 - некоторая величина, которая должна иметь наименование энергии, т. е. величина
- некоторая величина, которая должна иметь наименование энергии, т. е. величина 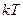 измеряется в единицах энергии.
измеряется в единицах энергии. 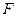 получило название свободной энергии.
получило название свободной энергии.
Тогда:
(**) 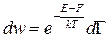 - распределение Гиббса.
- распределение Гиббса.
В 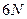 -мерном пространстве в каждый момент времени можно выделить точку, которая соответствует значениям координат и импульсов точек системы в этот момент времени.
-мерном пространстве в каждый момент времени можно выделить точку, которая соответствует значениям координат и импульсов точек системы в этот момент времени.
Т. к. частицы системы находятся в непрерывном хаотическом движении, то точка описывает некоторую траекторию в 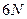 -мерном пространстве.
-мерном пространстве.
Распределение Гиббса – это есть вероятность того, что система попадает в объемчик 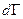 .
.
Если температура системы не меняется, и система является изолированной, то вероятность оказаться в любом объемчике 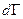 одинакова.
одинакова.
Проинтегрируем выражение (**):
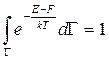 ( вытекает из того, что
( вытекает из того, что 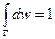 ).
).
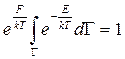 .
.
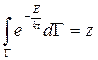 - интеграл состояния.
- интеграл состояния.
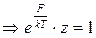 ,
,
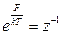 .
.
Проинтегрируем:
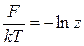 ,
,
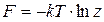 .
.
 2015-03-27
2015-03-27 484
484








