Обобщённая функция является обобщением классического понятия функции

Обобщённые функции впервые в науку были введены Дираком в его квантово-механических исследованиях, в которых систематически использовалась, так называемая, d - функция.

Обобщённая функция является обобщением классического понятия функции.

Постановка краевых задач характеризуется тем, что их решения предполагаются достаточно гладкими и удовлетворяют уравнению в каждой точке внутри области задания этого уравнения. Такие решения называются классическими, а постановка краевых задач – классической постановкой. Т.е., такая постановка предполагает, например, непрерывность правой части уравнения внутри области задания. Однако, в наиболее интересных задачах, эти правые части, характеризующие интенсивность внешних воздействий, имеют довольно сильные особенности. Поэтому, для таких задач классической постановки уже оказывается недостаточно. Чтобы поставить такие задачи, приходится отказываться (частично или полностью) от требования гладкости решения внутри области и вводить, так называемые, обобщённые решения. Но тогда встаёт вопрос, какие функции можно назвать решениями уравнений? Чтобы сделать это, необходимо существенно обобщить понятие производной и, вообще, понятие функции, т.е. ввести, так называемые обобщённые функции.

Понятие обобщённых функций**

Давно в физике употребляются сингулярные функции, которые не могут быть корректно определены в рамках классической теории функций. Простейшей сингулярной функцией является дельта-функция d (x - x₀ ), она по определению физиков равна нулю всюду, кроме одной точки x₀ , в этой точке равна ¥ и обладает интегралом равным 1.

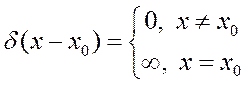
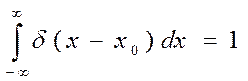
Эти условия не совместимы с точки зрения классического определения функции и интеграла.

В конкретных задачах такие функции нужны только на промежуточном этапе, в окончательном ответе они либо вовсе отсутствуют, либо фигурируют в произведении с какой-либо достаточно хорошей функцией. Поэтому нет необходимости отвечать на вопрос – что такое сингулярная функция? – сама по себе. Нам достаточно ответить на вопрос, что означает интеграл от произведения сингулярной функции и хорошей функции. Например, на вопрос, что такое d - функция, достаточно указать, что для любой достаточно хорошей функцией j (x) имеет равенство

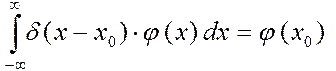
(1)

Иными словами, мы связываем с каждой сингулярной функцией функционал, который ставит в соответствие этой сингулярной и каждой, достаточно хорошей функциям, некоторое вполне определённое число. Например, для d - функции d (x-x₀ ), числом, которое ставится в соответствие каждой, достаточно хорошей функции j(x), есть значение j(x₀).

Таким образом, мы отождествляем сингулярную функцию с тем функционалом, о котором конкретно идёт речь и не задумываться об определении сингулярной функции. При этом, должен быть точно указан тот класс достаточно хороших функций, на котором задан этот функционал.

В эту схему также укладываются и обыкновенные интегрируемые функции: для каждой функции f (x) мы можем ответить на вопрос: чему равен интеграл от произведения f (x) на хорошую функцию. Таким образом, представление об обобщённых функциях, как о функционалах, охватывает как сингулярные, так и обыкновенные функции.