Выделим внутри движущейся жидкости элементарный параллелепипед АВСДА 1 В 1 С 1 Д 1 (рис. 3.4), через который протекает жидкость.
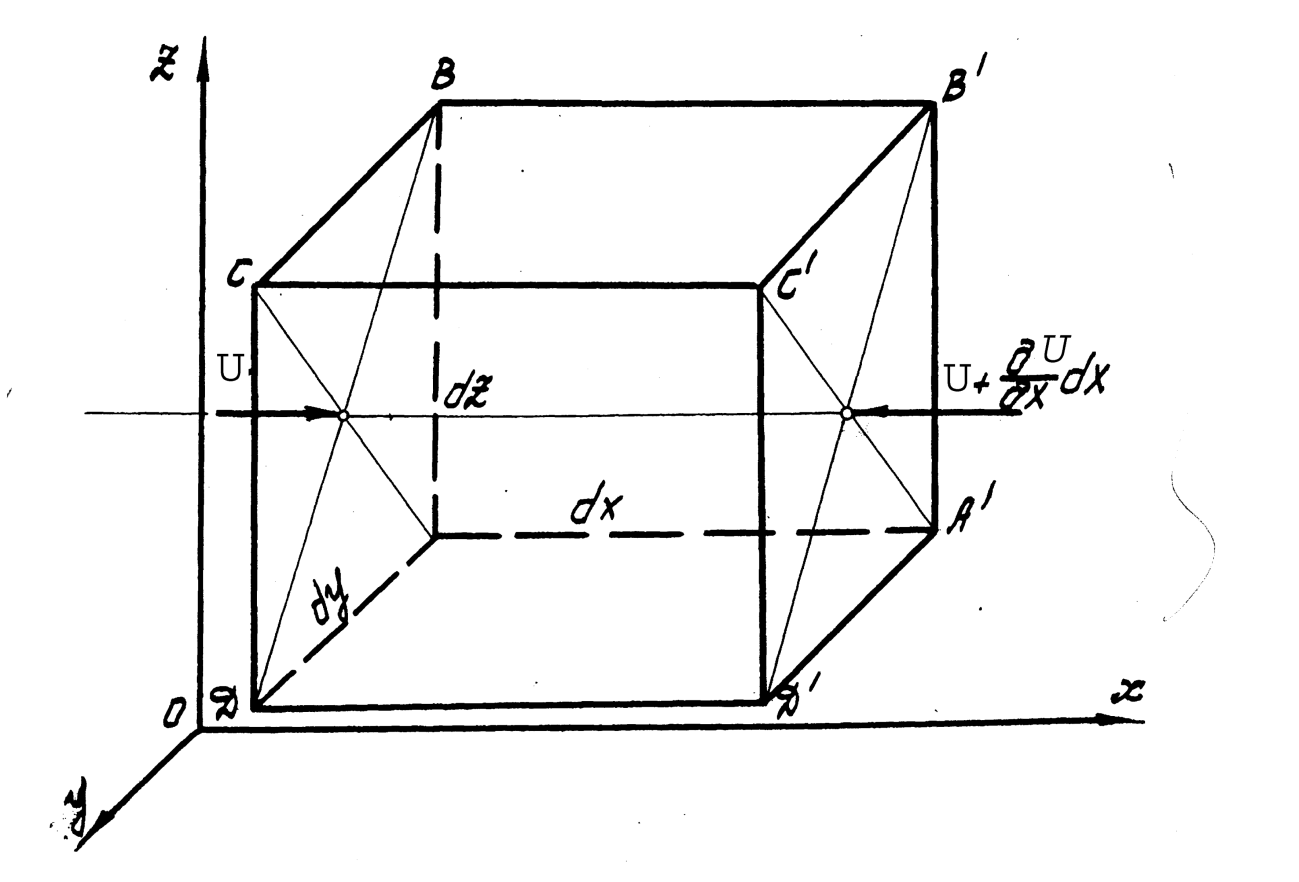 Рис. 3.4 Рис. 3.4
|
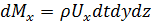 , а вытекает через правую грань А 1 В 1 С 1 Д 1 А 1масса
, а вытекает через правую грань А 1 В 1 С 1 Д 1 А 1масса
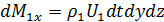 .
.
Плотность ρ и скорость U на входе в общем случае не равны плотности ρ 1 и скорости U 1 на выходе. При этом изменение ρ и U обусловлено изменением только координаты x, так как втекание и вытекание происходит одновременно. Поэтому
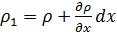 ;
; 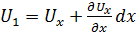 .
.
Следовательно,
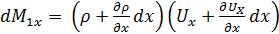 dtdydz=
dtdydz= 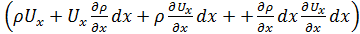 dtdydz.
dtdydz.
Но 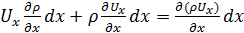 , а
, а 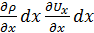 - величина высшего порядка малости относительно других слагаемых и ею можно пренебречь. Поэтому
- величина высшего порядка малости относительно других слагаемых и ею можно пренебречь. Поэтому
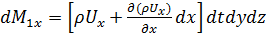 .
.
Изменение массы вследствие движения вдоль координатной оси ОХ
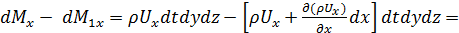
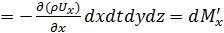 .
.
Аналогично найдем, что в итоге движения жидкости вдоль осей ОХ и ОZ изменение массы за время dt соответственно будет:
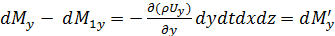 ;
;
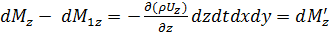 .
.
Следовательно, общее изменение массы за время dt:
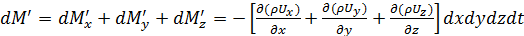 .
.
Это изменение массы равно изменению, обусловленному изменением плотности. В начальный момент времени tH масса внутри параллелепипеда
|
|
|
dMH =ρdxdydz.
К конечному моменту времени tК=tH+dt плотность изменяется. Это изменение происходит независимо от координат, поэтому
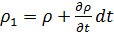 .
.
Следовательно, в конечный момент tК масса жидкости в параллелепипеде
dMК = 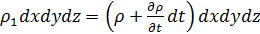 .
.
Таким образом, приращение массы за время dt из-за изменения плотности:
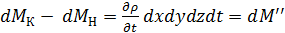 .
.
При условии неразрывности 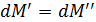 , т. е.
, т. е.
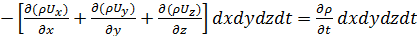 ,
,
или после сокращения на dxdydzdt
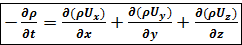 . (3.15)
. (3.15)
Выражение (3.15) - искомое уравнение неразрывности. При установившемся движении плотность от времени не зависит и 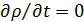 . Поэтому уравнение неразрывности примет вид
. Поэтому уравнение неразрывности примет вид
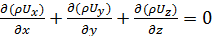 . (3.16)
. (3.16)
Для несжимаемой жидкости (ρ = const) уравнение неразрывности
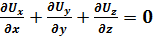 . (3.17)
. (3.17)
Неразрывность движения применительно к струйке жидкости (рис. 3.3). Выделим в струйке бесконечно близкими сечениями dω 1 и dω 2, находящимися на расстоянии dS друг от друга, объем
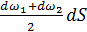 .
.
Масса жидкости, вошедшая в рассматриваемый объем через сечение dω 1 в течение промежутка времени dt при расходе в струйке dQ, равна ρdQdt. Масса, вышедшая через противоположное сечение dω 2, равна
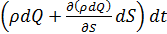 .
.
Разность поступающей и вышедшей масс должна, очевидно, равняться изменению за тот же промежуток времени массы ρdωdS,первоначально заключавшейся в выделенном объеме, то есть
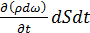 .
.
Следовательно,
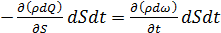 ,
,
откуда
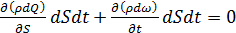 ,
,
или
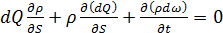 . (3.18)
. (3.18)
В случае мало сжимаемой жидкости изменением плотности ρ вдоль пути dS можно пренебречь (считать, что 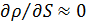 ) и придать уравнению неразрывности более простой вид:
) и придать уравнению неразрывности более простой вид:
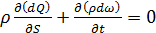 . (3.19)
. (3.19)
Для несжимаемой жидкости (ρ=const) уравнение неразрывности ещё проще:
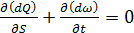 . (3.20)
. (3.20)
В случае, когда 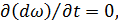
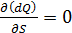 , (3.21)
, (3.21)
откуда dQ =const или, так как dQ=Udω,
Udω = const. (3.22)
Таким образом, объемный расход жидкости остается неизменным на всем протяжении элементарной струйки.
|
|
|
Так как расход потока жидкости равен сумме расходов элементарных струек, условие сплошности (неразрывности) потока для несжимаемой жидкости можно записать в виде
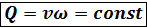 .(3.23)
.(3.23)
Для двух живых сечений потока уравнение (3.23) можно записать в виде
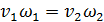 . (3.23а)
. (3.23а)
Равенство (3.23а) называют уравнением неразрывности в форме Леонардо да Винчи.
Литература по содержанию лекции:
1. Чугаев Р. Р. Гидравлика (Техническая механика жидкости). - Л.: Энергоиздат, 1982. - 672 с.
2. Штеренлихт Д. В. Гидравлика. - М.: Энергоатомиздат, 1985. - 640 с.
3. Гиргидов А. Д. Механика жидкости и газа (гидравлика): Учебник для вузов. СПб.: Изд-во СПбГПУ, 2002. - 545 с.
 2015-03-27
2015-03-27 670
670








