Задание 4.1

4.1.Доказать, что если функция u(x,y,z) удовлетворяет уравнению Лапласа

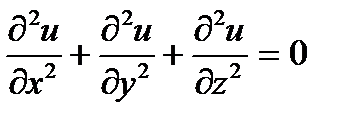
то

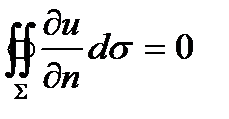
где 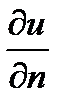- производная по направлению внешней нормали к кусочно гладкой замкнутой поверхности Σ.

4.2.Доказать, что если функция u(x,y,z) является многочленом второй степени и Σ – кусочно-гладкая замкнутая поверхность, то интеграл

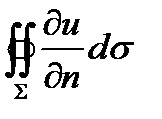
пропорционален объёму, ограниченному поверхностью Σ.

4.3.При какой функций 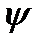(r) будет div 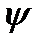(r)r =2 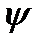(r)

4.4. Найти div (r⁴ r)

4.5. Найти дивергенцию векторного поля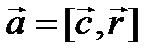

4.5. Найти div (r[w, r]) где w –постоянный вектор

4.6. При какой функции 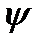(z) дивергенция поля 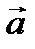= xzi+yj+ 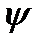(z)k будет равна z

4.7. Найти поток радиуса вектора r через поверхность сферы

4.8. Электростатическое поле точечного заряда q равно 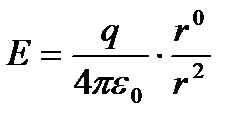. Вычислить div E

4.9.Показать, что 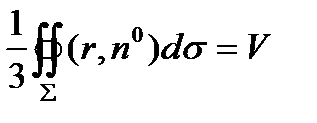где V –объем, ограниченный замкнутой поверхностью S

4.10.Доказать, что если S -замкнутая кусочно гладкая поверхность и 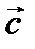–ненулевой постоянный вектор, то 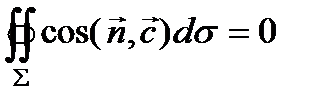где 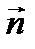–вектор, нормальный к поверхности S

4.11.Доказать формулу 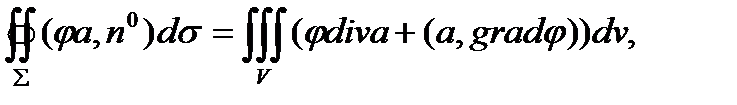где j=j(x,y,z), а S -поверхность, ограничивающая объем V. Установить условия применимости формулы.

4.12.Найти дивергенцию векторного поля 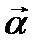=xyi+xyi+zk в точке Р(1,2,-1)