Свойства градиента

1⁰  Градиент направлен по нормали к поверхности уровня (или к линии уровня, если поле плоское).

2⁰  Градиент направлен в сторону возрастания функции поля.

3⁰  Модуль градиента равен наибольшей производной по направлению в данной точке поля:

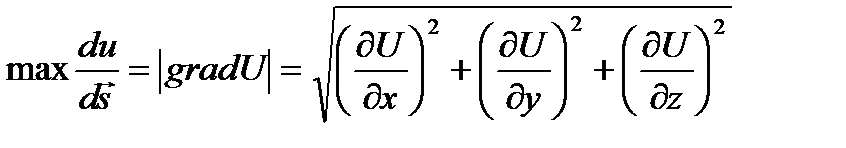
Эти свойства дают инвариантную характеристику градиента. Они говорят о том, что вектор gradU указывает направление и величину наибольшего изменения скалярного поля в данной точке.

Замечание 2.1. Если функция U(x,y) есть функция двух переменных, то вектор

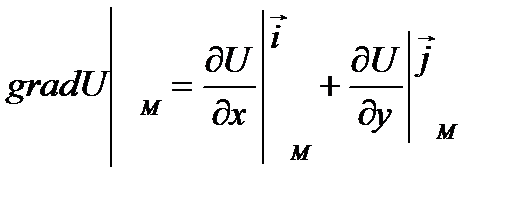(2.3)

лежит в плоскости oxy.

Пусть U=U(x,y,z) и V=V(x,y,z) дифференцируемых в точке М₀ (x,y,z) функции. Тогда имеет место следующие равенства:

а) grad(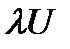)= 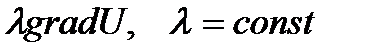; б) grad(UV)=VgradU+UgradV;

в) grad(U 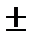V)=gradU 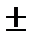gradV; г) г) grad 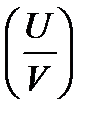= 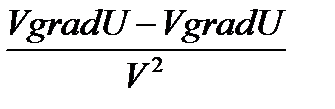, V ;

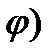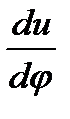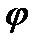
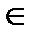
д) gradU( = gradU, где 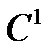, U=U(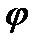) имеет производную по .

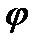Пример 2.1. Дана функция U=x²+y²+z². Определить градиент функции в точке М(-2;3;4).

Решение. Согласно формуле (2.2) имеем

,

.

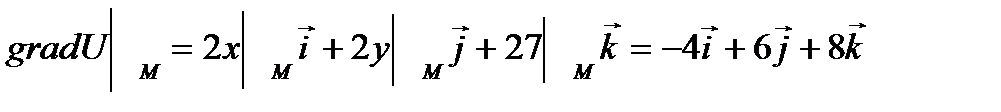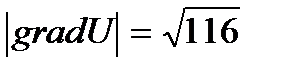Поверхностями уровня данного скалярного поля являются семейство сфер x²+y²+z² , вектор gradU=(-4;6;8) есть нормальный вектор плоскостей.

Пример 2.2. Найти градиент скалярного поля U=x-2y+3z.

Решение. Согласно формуле (2.2) имеем

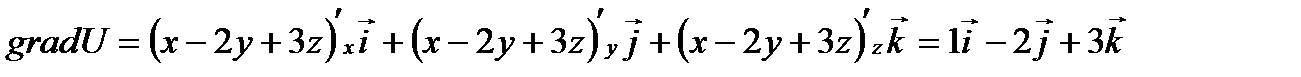
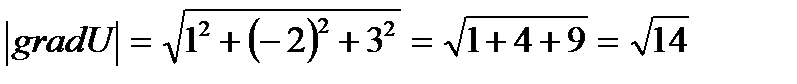
Поверхностями уровня данного скалярного поля являются плоскости

x-2y+3z=С; вектор gradU=(1;-2;3) есть нормальный вектор плоскостей этого семейства.

Пример 2.3. Найти наибольшую крутизну подъема поверхности U=x^y в точке М(2;2;4).

Решение. Имеем: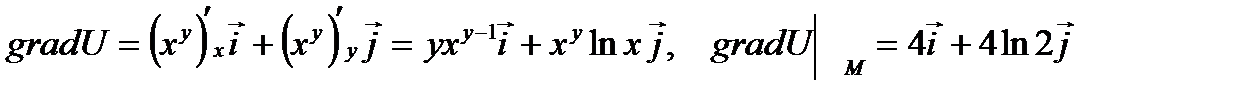

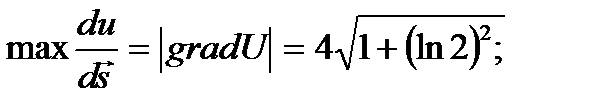
Пример 2.4. Найти единичный вектор нормали к поверхности уровня скалярного поля U=x²+y²+z².

Решение. Поверхности уровня данного скалярного Поля-сфера x²+y²+z²=С (С>0).

Градиент направлен по нормали к поверхности уровня, так что

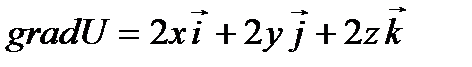. Определяет вектор нормали к поверхности уровня в точке М(x,y,z). Для единичного вектора нормали получаем выражение

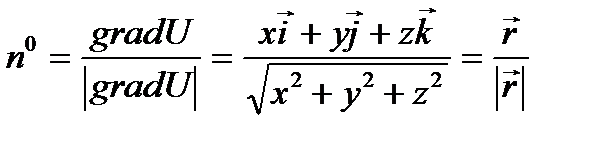, где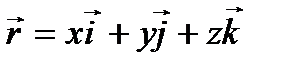

.

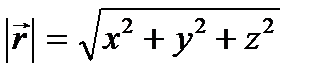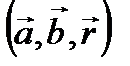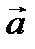Пример 2.5. Найти градиент поля U= , где и 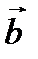постоянные векторы, r –радиус вектор точки.

Решение. Пусть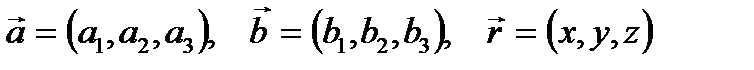

Тогда: 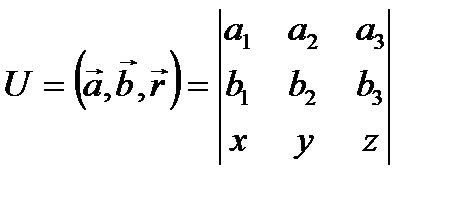. По правилу дифференцирования определителя получаем

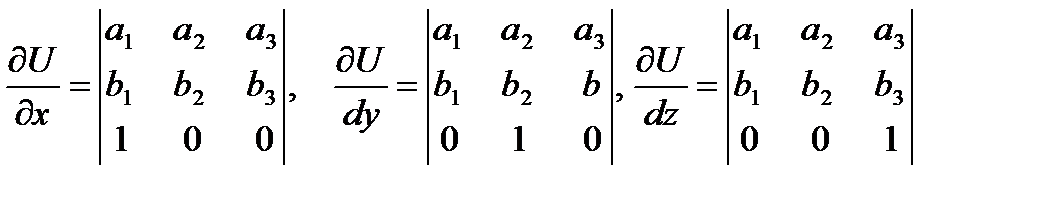
Следовательно,

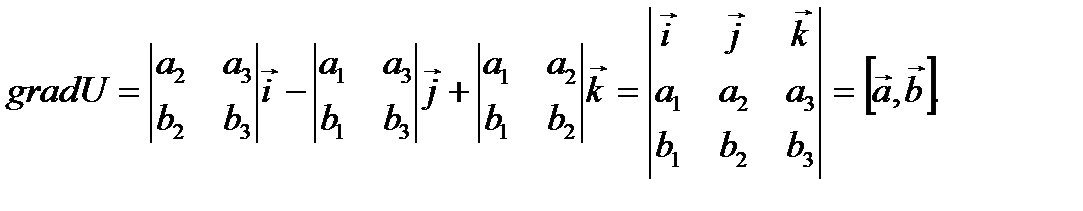
Пример 2.6. Найти градиент расстояния 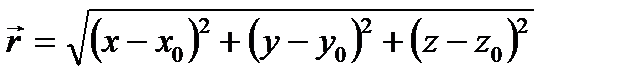, где P(x,y,z) - изучаемая точка поля, P₀(x₀,y₀,z₀) - некоторая фиксированная точка.

Решение. Имеем 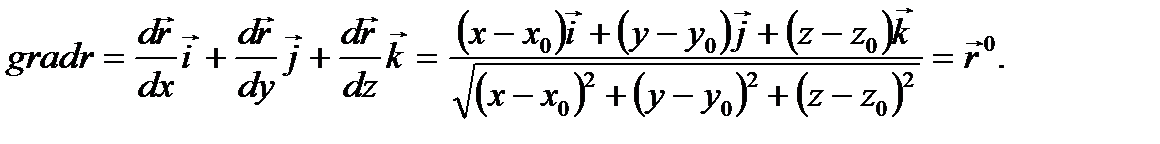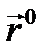- единичный вектор направления .

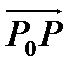Пример 2.7. Найти угол 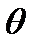между градиентами функций 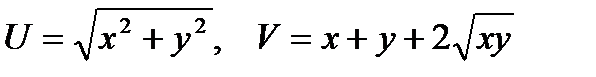в точке М₀(1,1).

Решение. Находим градиенты данных функций в точке М₀(1,1), имеем

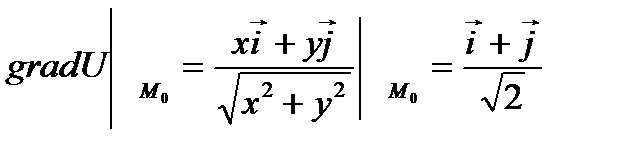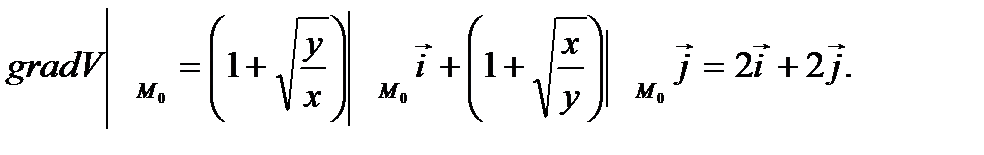; Угол между gradU и gradV в точке М₀ определяется из равенства

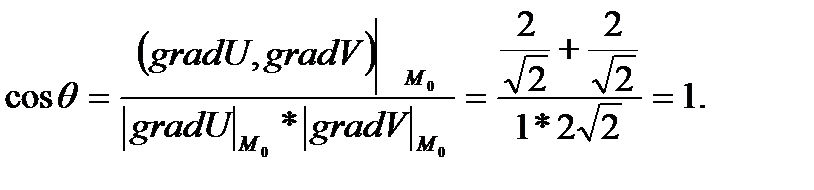Отсюда 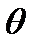=0.

Пример 2.8. Найти производную по направлению, радиус- вектор 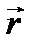равен

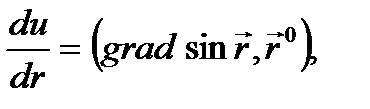(2.4)

Решение. Находим градиент этой функции:

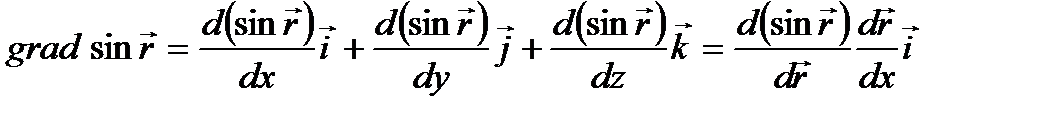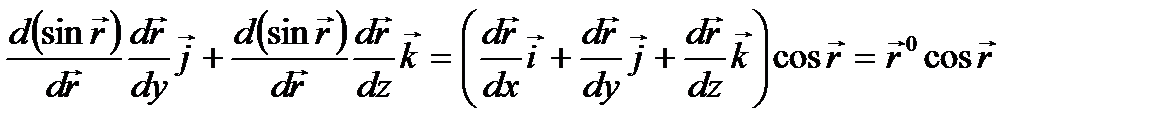+ (2.5)

Подставляя (2.5) в (2.4), получим

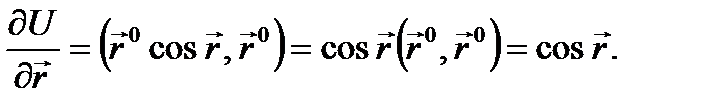
Пример 2.9. Найти в точке М₀(1;1;1) направление наибольшего изменения скалярного поля U=xy+yz+xz и величину этого наибольшего изменения в этой точке.

Решение. Направление наибольшего изменения поля указывается вектором grad U(M). Находим его: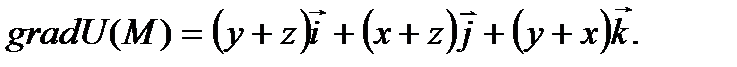

И, значит, 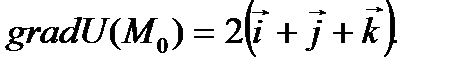. Это вектор определяет направление наибольшего возрастания данного поля в точке М₀(1;1;1). Величина наибольшего изменения поля в этой точке равна

.

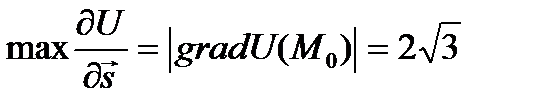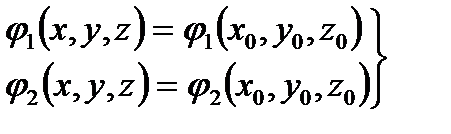
Пример 3.1. Найти векторные линии векторного поля 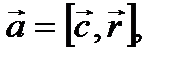где 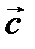-постоянный вектор.

Решение. Имеем 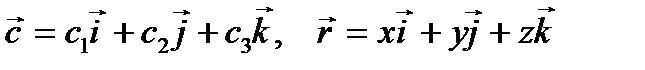так что

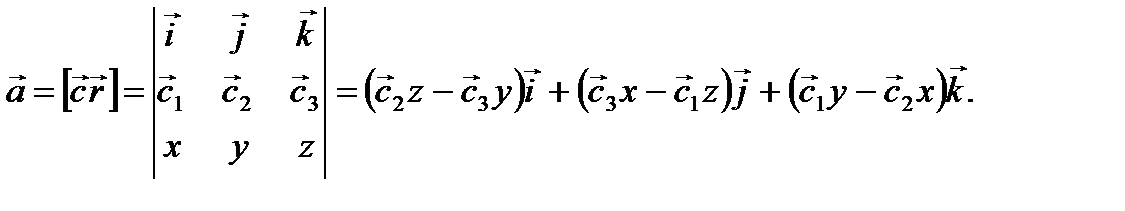Дифференциальные уравнения векторных линий

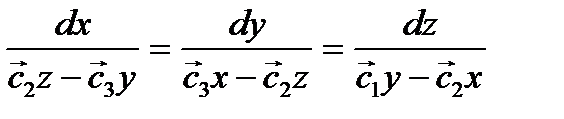(3.3)

Умножим числитель и знаменатель первой дроби на х, второй-на у, третий-на z и сложим почленно. Используя свойство пропорций, получим

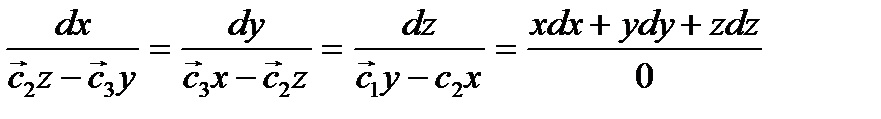, отсюда xdx+ydy+zdz=0, а значит

x²+y²+z²=A₁, A₁-const>0. Умножив теперь числитель и знаменатель первой дроби (3.3) на с₁, второй –на с₂, третий на с₃ и сложив почленно, получим

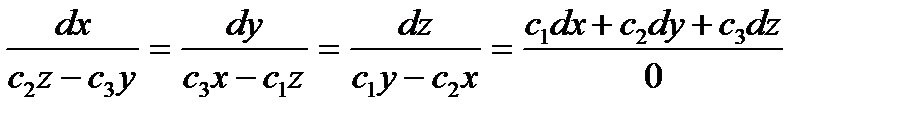, откуда с₁dx+c₂dy+c₃dz=0

И, следовательно, с₁x+c₂y+c₃z=A₂. A₂-const.

Искомые уравнения векторных линий

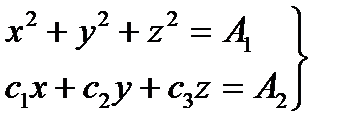
Эти уравнения показывают, что векторные линии получаются в результате пересечения сфер, имеющих общий центр в начале координат, с плоскостями, перпендикулярными вектору 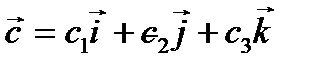. Отсюда следует, что векторные линии являются окружностями, центры которых находятся на прямой, проходящей через начало координат в направлении вектора с. Плоскости окружностей перпендикулярны указанной прямой.

Пример 3.2. Найти векторную линию поля 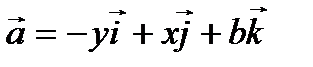проходящую через точку (1,0,0).

Решение. Дифференциальные уравнения векторных линий

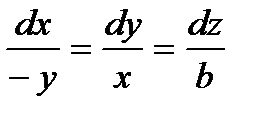отсюда имеем 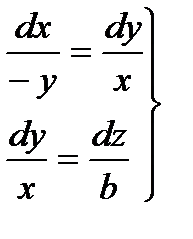. Решая первое уравнение 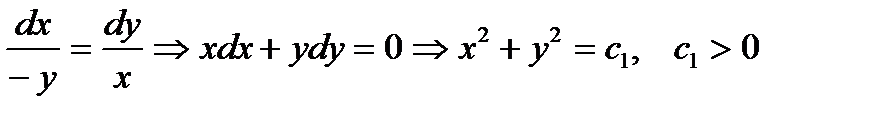. Или если ввести параметр t, то будем иметь 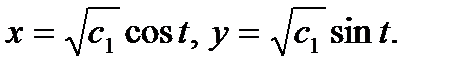В этом случае уравнение 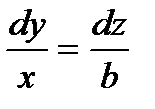принимает вид 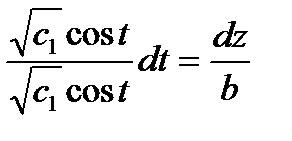или dz=bdt, откуда z=bt+c₂.