2015-03-07
1258
Определение 5.1. Если во всех точка М некоторой области G дивергенция векторного поля (заданного в области G) равна нулю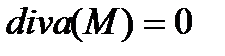 
то говорят, что поле соленоидально в этой области.
Таким образом, по определению, соленоидальное поле не имеет источников и стоков.
Из теоремы Гаусса – Остроградского следует, что в соленоидальном поле поток вектора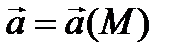 
через любую замкнутую поверхность σ, лежащую в этом поле, равен нулю.
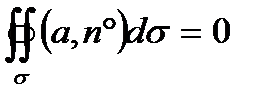
В соленоидальном поле G векторные линии не могут ни начинаться, ни кончаться. Они могут быть либо замкнутыми кривыми, либо иметь концы на границе поля.
Уравнение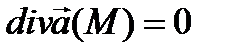 
называется в гидродинамике уравнением неразрывности несжимаемой жидкости.
В этом случае количество жидкости, выходящей через какую – нибудь замкнутую поверхность σ, всегда равняется количеству входящей жидкости, и полный поток равен нулю.
Пусть имеем поле вектора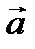 
(М) (не обязательно соленоидальное). Рассмотрим в поле замкнутый ориентированный контур L. Поверхность Σ, имеющую линию L своим краем, назовем поверхностью, натянутой на контур L. Нормаль n к поверхности Σ условимся ориентировать так, чтобы из конца нормали выбранный обход контура L был виден совершающимся против часовой стрелки (рис. 5.1).
| nº Σ L |
Рис. 5.1
