2015-03-07
890
Рассмотрим дифференциальное уравнение
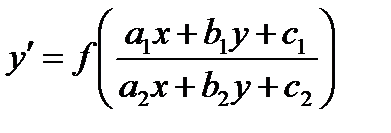(8.22)
Уравнение (8.22) приведем к однородному уравнению. В случае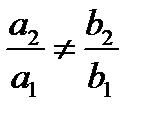 
приводится к однородным уравнением с помощью замены переменной
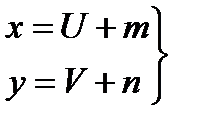(8.23)
Где n и m находится из системы уравнений
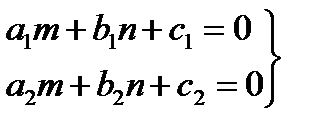(8.24)
Поскольку здесь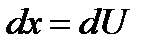 
, то уравнение (8.22) преобразуется к виду
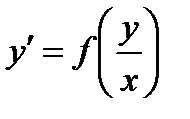относительно функции 
.
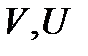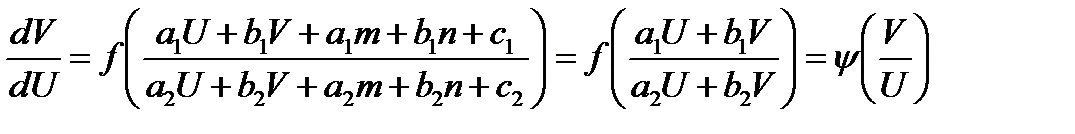
Пример8.13: Решить уравнение
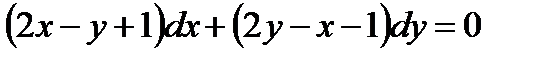(8.25)
Решение: так как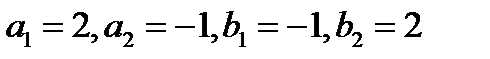 
и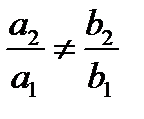 
; 
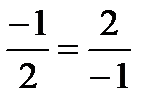тогда в силу системы (8.24) имеем:
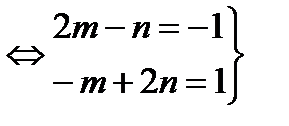(8.24΄)
Решая систему (8.24΄) находим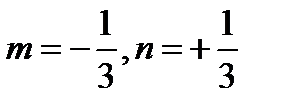 
.
Следовательно,
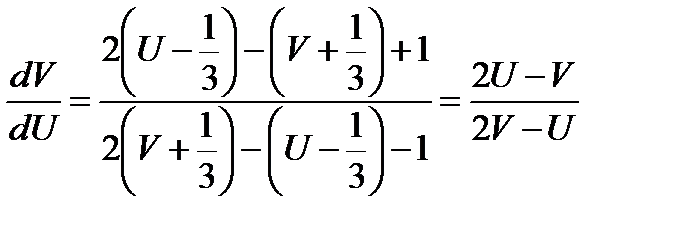
Отсюда видно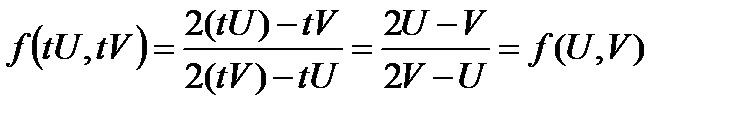 
.
То есть функция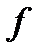 
является однородной, следовательно (8.24) приведена к однородным уравнением. Полагаем 
.
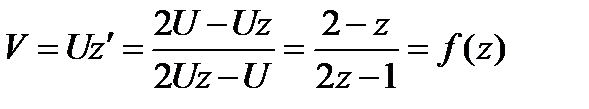Согласно формуле (8.24), имеем
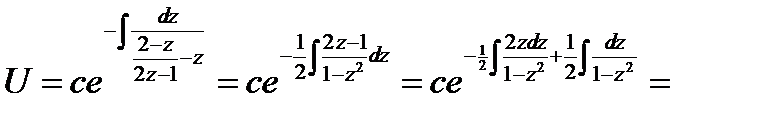
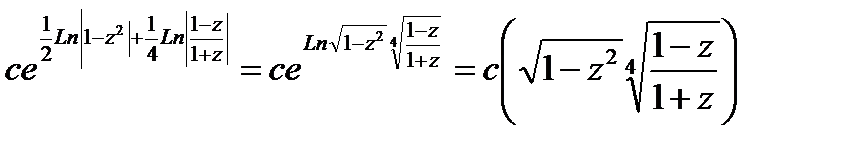
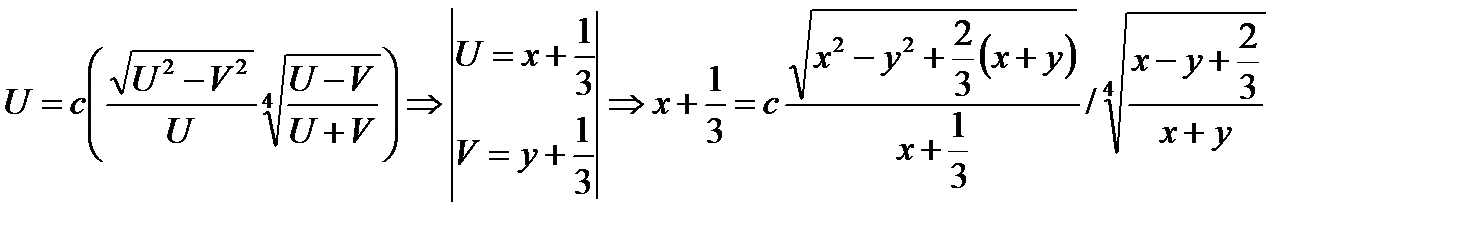
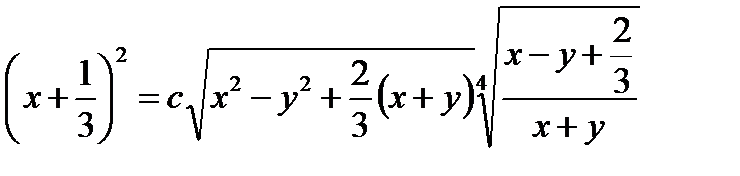
Если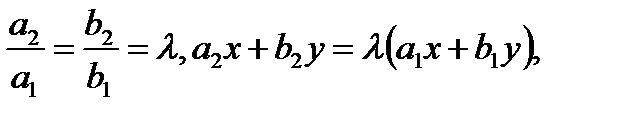 
То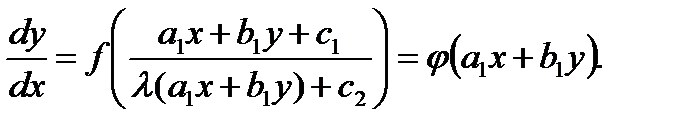 
Делая подстановку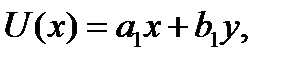 
уравнение сходится к разделяющимся переменным.
