Уравнение (9.2) решается методом Бернулли, который заключается в следующем. Будем искать решение в виде произведения двух функций.
у(х) = u(x)v(x) (9.4)
имеем
y'(x)=u'(x)v(x)+v'(x)u(x) (9.5)
Подставляя (9.4) и (9.5) в (9.2), получим
u'(x)v(x) + u(x)v'(x) + p(x)u(x)v(x) = f(x) или
u(v'(x)+p(x)v(x)) + u'(>)v(x)=f(x) (9.6)
Подберем функцию v так, чтобы v'(x) + p(x)v = 0. Тогда относительно v(x) имеем линейное однородное уравнение
v'(x) + p(x)v(x) = 0 (9.7)
которое является уравнением с разделяющимися переменными, разделив переменные, получим
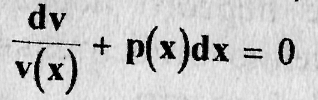
Следовательно, по формуле (8.10) имеем
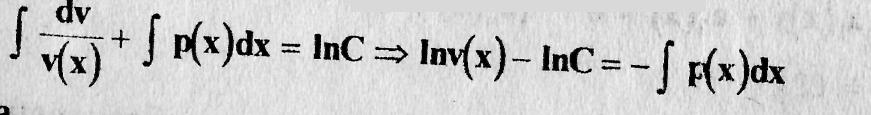
откуда
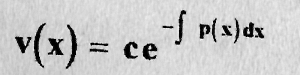 (9.8)
(9.8)
Для удобства в формуле учитывая (9.7), имеем
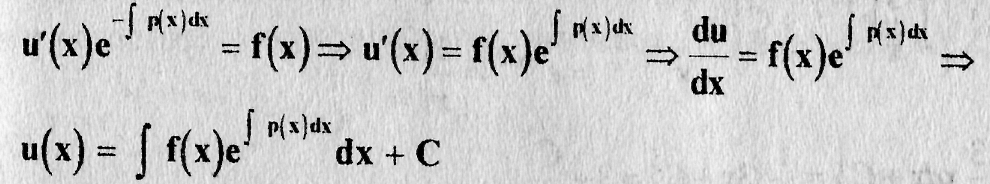 (9.9)
(9.9)
следовательно, общее решение уравнения (9.2) запишется в виде
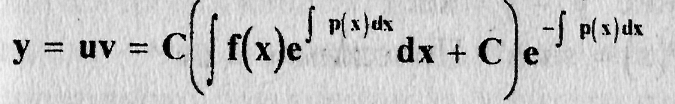 (9.10)
(9.10)
где с- произвольная постоянная.
Входящие в формулу (9.10) интегралы обозначают-производные, но выбранные определенно первообразные от подынтегральных функций. Удобно эти первообразные взять в виде определенных интегралов с переменным пределом х и нижним фиксированным пределом х0, принадлежащим (а,b). Тогда формула (9.10) примет вид
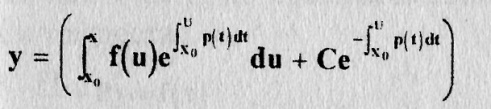 (9.11)
(9.11)
Если потребовать, чтобы при х = х0 решение обратилось в Уо(у(хо) = Уо). тo очевидно, получим у0 = С.
Следовательно, решение задачи Коши (у(х0) = у0) для дифференциального уравнения (9.2) дается формулой
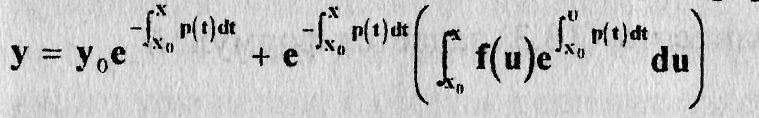 (9.12)
(9.12)
формула (9.10) показывает, что общее решение линейного неоднородного уравнения равно сумме решения соответствующего однородного уравнения и частного решения однородного уравнения (получающегося из (9.10) при с=0).
Пример 9.1: Решить уравнение
ху' + у - 3 = 0 (9.13)
Решение: Так, как уравнение (9.13) имеет вид (9.1), где ао(х) = х, а,(х) = 1, а2(х) = -3 и, разделив на х, получим уравнение вида (9.2), то есть
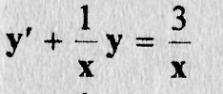 (9.14)
(9.14)
где 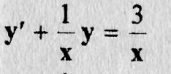 и применяя формулу (9.10), получим
и применяя формулу (9.10), получим
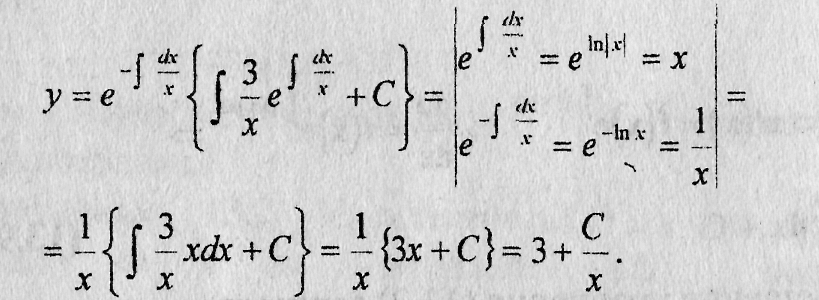
Пример 9.2: Решить уравнение у'-у= sin x. Решение: Здесь р(х) = -1, f(x) = sin х Положим у = uv
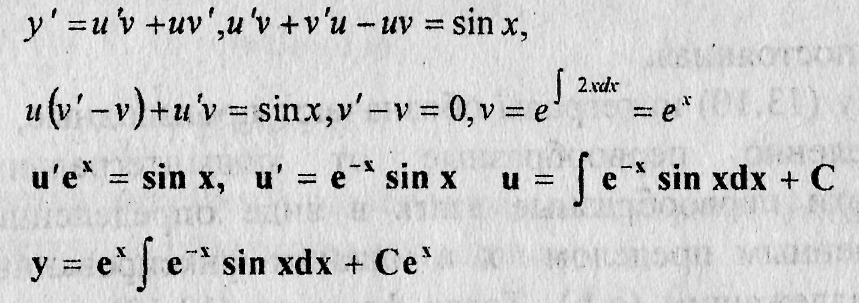
интегрируя no частям, находим что
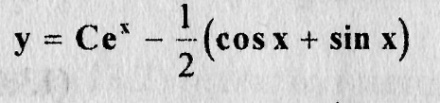
 2015-03-07
2015-03-07 605
605








