Промежуточные интегралы

Если мы имеем уравнение n-го порядка

F(x, y, y',…у ⁿ)=0 (12.1)

Как известно, что соотношение

Φ(x, y, С₁, С₂, …,С _n)=0 (12.1^/)

определяющее решение этого уравнения и связывающее у,х и п существенных произвольных постоянных, называется общим интегралом (12.1). Иначе, общий интеграл можно определить так: соотношение (12.1^/) называется общим интегралом уравнения (12.1), если, исключая из него и из уравнений, получаемых дифференцированием его по х, произвольные постоянные С₁, С₂, …,С n, мы приходим к уравнению (12.1).

Пусть теперь мы имеем соотношение:

Ψ(x, y, у '…. у ⁿ, С₁, С₂, …,С _n)=0 (12.2)

в которое входит производные до n-го порядка и n-к произвольных постоянных. Дифференцируем теперь это уравнение n-к раз по х, считая у функцией х, имеем

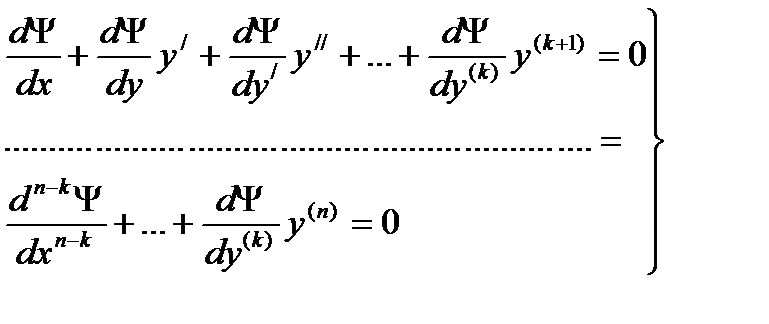(12.2^/)

Если в результате исключения из n-к+1 уравнений (12.2) и (12.2') n-к постоянных Сi (i=к+1,к+2,,,,n) мы получим уравнение (12.1), то соотношение (12.2/) называется промежуточным интегралом уравнения (12.1). В частности, если соотношение (12.2^/) содержит только одно произвольное, то есть имеет вид

Ψ(x, y, у ',у″,…. у ⁿ, С)=0

то оно называется первым интегралом уравнения (12.1)

Пример12.1: Составить дифференциальное уравнение, если У=e^Cx→y-e^Cx=0→F(x,y,C)=0

Решение: y^/=Ce^Cx→y^/=Cy, C= ;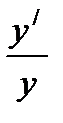

Откуда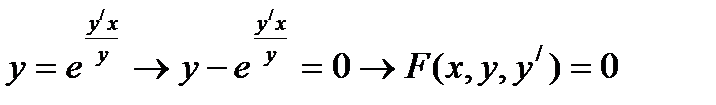

Промежуточный интеграл (12.2), если в нем рассматривать у как искомую функцию, сам является дифференциальным уравнением порядка К, где к<n. Легко видеть, что каждое решения уравнения (12.2) является решением уравнения (12.1). В самом деле, если у=φ(x) есть решение уравнения (12.2), то поставляя это значение у в уравнение (12.2) и (12.2'), мы обратим их в тождества: а значит и уравнение (12.1), которое является следствием системы (12.2) и (12.2'), обратимся в тождество,что требовалось доказать. Если мы найдем общее решение уравнения (12.2), то оно должно содержать к новых произвольных постоянных С₁, С₂, …,С_к сверх входящих в самое уравнение параметров С_к+1, …С._n и мы получим решение уравнения (12.2), содержащее n произвольных постоянных, то, есть общее решение этого последнего уравнения.

Таким образом, знания промежуточного интеграла вида (12.2) позволяет свести задачу интеграции уравнения n-го порядка к интеграции уравнения порядка к-n то есть к задаче теоретически говоря, более простой.