Пусть уравнение (12.1), то есть уравнение вида
F(x,y,y',y″,...yⁿ)=0 (12.1)
не содержит явно независимого переменного х, то есть
F(y,y',y″,...yⁿ)=0 (12.10)
Здесь мы проведем такую замену переменных: в качестве новой искомой функции вводим
Z=dy/dx; за независимое переменное принимает у.
Вычисляем в этом предположении производные различных порядков
y'=z(y);
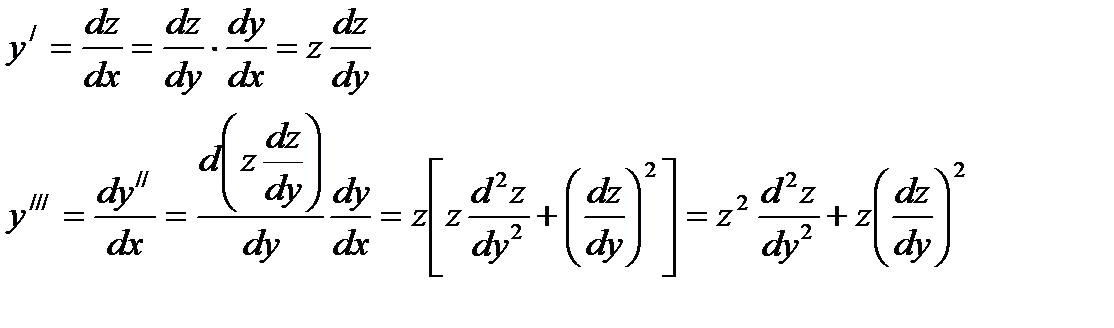
Таким образом,вторая производная от у по х выражается через z и dz /dу, третья производная выражается через z его производные не выше второго порядка. Легко доказать методом полной индукции, что 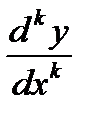 выражается через
выражается через 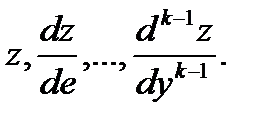 Подставляя выражения для у″, у″',...yⁿ в новых переменных в уравнение (12.10), получим новое дифференциальное уравнение порядка n-1
Подставляя выражения для у″, у″',...yⁿ в новых переменных в уравнение (12.10), получим новое дифференциальное уравнение порядка n-1
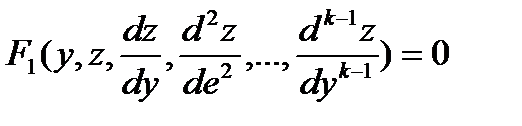 (12.11)
(12.11)
Если его удастся по интегрировать, то его общий интеграл Φ(y,z,С1,С2,...Сn-1)=0 или Ф (у, dy/dx, С1,С2,...Сn-1 )=0
который является промежуточным для уравнения (12.10), дает дифференциальное уравнение первого порядка, интегрируемое в квадратурах.
Рассмотрим частный случай, то есть уравнение вида
Y″=f(x, y') или F(y, y',y″)=0 (12.10/)
Для его решения снова положим
y'=z(y) (12.12)
у// = z(dz/dy) (12.12/)
(12.12) и (12.12') подставляя в уравнение (12.10') получим уравнение первого порядка относительно вспомогательной функции z
z *d z /dу =f(y,z), (12.13)
интегрируя его, найдем z как функцию от у и произвольного с,
z=Р(у,с,),
подставляя в (12.2) получим дифференциальное уравнение первого порядка дляфункции у от хdy\dx =р(у,с,) разделяя переменные находим 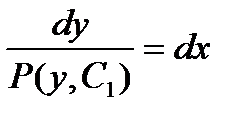 , интегрируя это уравнение, получим общий интеграл исходного уравнения: ф(х,у,с 1,с 2)=0
, интегрируя это уравнение, получим общий интеграл исходного уравнения: ф(х,у,с 1,с 2)=0
Пример:12.4: Решить дифференциальное уравнение уу″-y²=у4 или 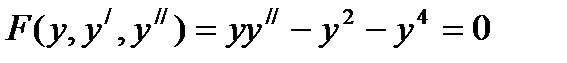
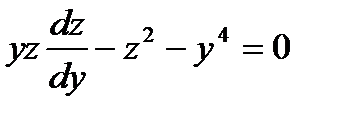
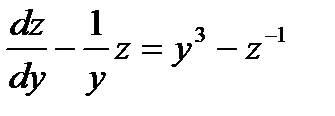
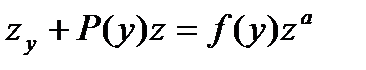
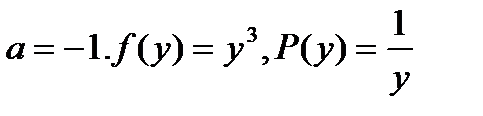
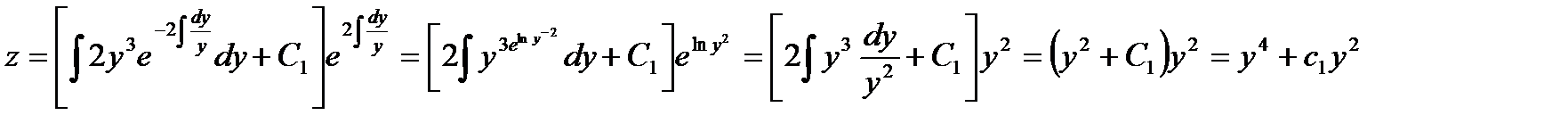
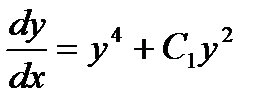
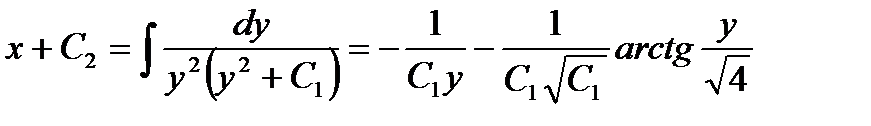
 2015-03-07
2015-03-07 1856
1856








