Уравнение
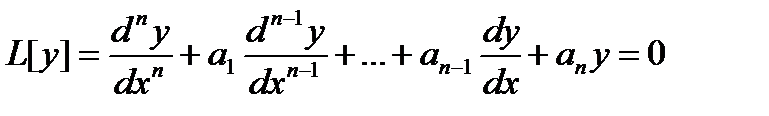
или
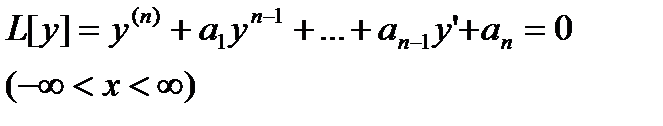 (13.1)
(13.1)
где а1=const(i=ln) —постоянные числа, называется линейным однородным дифференциальным уравнением п —го порядка с постоянными коэффициентами.
Мы покажем, что в таком случае интеграция уравнения (13.1) всегда возможна в элементарных функциях и сводится даже не к квадратурам, а к алгебраическим операциям.
Заметим, что в силу общих свойств линейных уравнений, нам достаточно найти n —частных решений, у1(х), у2(х),...уn(х) образующих линейно независящую систему не на всей оси (фундаментальную систему), тогда общее решение уравнения (13.1) будет иметь вид [Лекция 11. Теорема 11.3]
у=С1у1+С2у2 +...Сnyn= 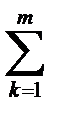 Скук (13.2)
Скук (13.2)
Будем искать частные решения уравнения (13.1) в виде
у = еkx (13.3)
где к- постоянное, которое мы можем выбирать произвольно Дифференцируя по х выражение (13.3) один раз, два раза, n-раз мы получим следующую функцию:
у'=кекx,у" = 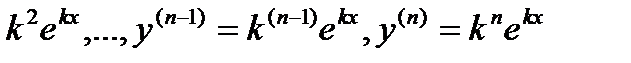 (13.4)
(13.4)
Внося выражение (13.3) и (13.4) в левую часть уравнения (13.1), которую мы обозначим символом оператора L, мы получим:
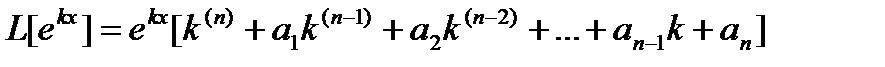 (13.5)
(13.5)
В равенстве (13.5), в правой части, в скобках стоит многочлен n-ой степени относительно к с постоянными коэффициентами. Она называется характеристическим многочленом, соответствующим оператору L; обозначим его через F (к)
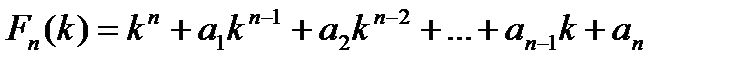
В этих обозначениях равенство (13.5) кратко запишется так
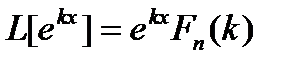 (13.5')
(13.5')
Заметим, что характеристический многочлен получается из оператора L [у], если производные различных порядков в этом последнем равенстве заменить равными степенями величины к. Если выражение (13.3) есть решение дифференциального уравнения (13.1), то выражение (13.5) должно тождественно обращаться в нуль, но множитель  .. Следовательно, мы должны положить
.. Следовательно, мы должны положить
Fп(к) = кn+a1кn-1+а2кn-2 + …+aп-1к + ап =0 (13.6)
Равенство (13.6) есть алгебраическое уравнение с неизвестным к. Она называется характеристическим уравнением. Если мы в качестве постоянного к в выражении (13.3) возьмем корень к, характеристического уравнения (13.6), то выражение (13.5) будет тождественно равно нулю, т.е. еk1x будет являться решением дифференциального уравнения.
Но характеристическое уравнение n-ой степени, следовательно но имеет n корней.
1. Пусть корни характеристического уравнения (13.6) действительные и различные, то есть
к1,к2,...,кп (1 3.7)
каждому из корней (13.7) соответствует частное решение дифференциального уравнения (13.1)
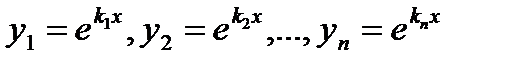 (13.8)
(13.8)
Докажем, что эти решения образуют фундаментальную систему. Для этого составим определитель Вронского

Последний определитель есть известный определитель Вандермонда, он равен
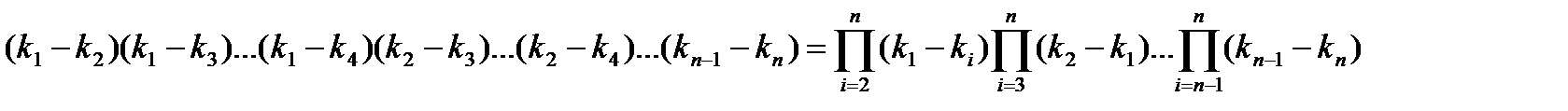
и следовательно, не обращается в нуль, если все корни уравнений (13.6) различны. Таким образом, система решений (13.8) является фундаментальной, и общее решение уравнения (13.1) будет
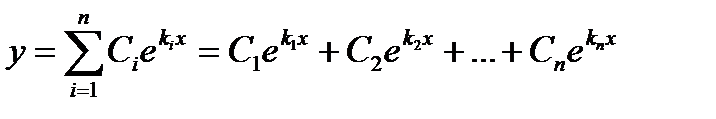 (13.9)
(13.9)
где С1, С2,... Сn, произвольные постоянные.
Пример 13.1: у''-у=0 характеристическое уравнение есть к2-1=0.
Его корни различны и равны соответственно к1=1, к2=-1. Отсюда следует, что соответствующие частные решения будут таковы: y1 =eх, у2=e-x. А тогда общее решение есть у=С1ех+С1е-x
Пример 13.2: у'''-2у''-у/+2у=0.
Составим характеристическое уравнение k3-2k2-k+2=0. Его преобразуем к следующему виду
k2(к-2)-(к-2)=(к-2)(к2-1)=(к-2)(к-1)(к+1)=0. Отсюда корни различные и равны соответственно к1=1, к2=-1, к3=2. Тогда соответствующие частные решения будут таковы y1=ех, у2=е-x, у3=е2x. Следовательно, общее частное решение есть у=С1ех+С}2е-x+С3е 2x.
2. Пусть корни характеристического уравнения (13.6) являются комплексными. Тогда заметим, что, в силу того, что коэффициенты уравнений (13.6) действительны, и комплексному корню 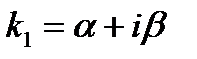 соответствует другой корень
соответствует другой корень 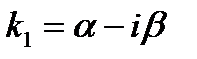 .Если мы напишем решение у1, соответствующее корню к1 то оно будет вид
.Если мы напишем решение у1, соответствующее корню к1 то оно будет вид
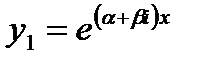 (13.10)
(13.10)
Выражение (13.10) является, вообще говоря, комплексным числом; мы имеем дело с комплексной функцией действительного переменного х.
Всякая комплексная функция f (х) действительного переменного может быть представлена в виде
f(х)=и(х)+iv(х) (13.11)
где и(х), v\(х) —две действительные функции действительного переменного и обратно, две производные действительные функции и(х),v(х) дают по формуле (13.11) комплексную функцию действительного переменного. Докажем следующую лемму.
Лемма 13.1. Если мы имеем комплексное решение вида (13.11) линейного дифференциального уравнения с действительными (не обязательно постоянными) коэффициентами
L[y]=0,
То функции и(х), v(х) в отдельности являются решением (действительными) уравнения (13.12).
Доказательство: Действительно из свойства линейного дифференциального оператора L[у] следует
L[u(х)+iv(х)]=L[u(х)]+iL[v(х)] (13.13)
По условию леммы, выражение (13.13) тождественно равно нулю, то есть
L[u(х)]+iL[v(х)]=0,
но оба выражения L[u] и L[v] суть действительные функции от х тождественное равенство выражения (13.13) влечет за собой, таким образом, два тождества
L[u(х)]=0, L[v(x)]=0, что доказывает лемму.
Воспользуемся леммой (13.1) для преобразования решения (13.10).
Отделяя в нем действительную часть от мнимой по формуле
Эйлера получаем
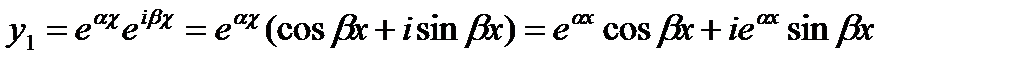
Согласно леммы, мы получаем: комплексному корню 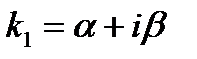 соответствуют два действительных решения уравнения (13.1').
соответствуют два действительных решения уравнения (13.1').
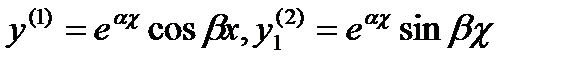 (13.13')
(13.13')
Заметим, что сопряженному корню 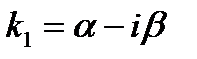 соответствует комплексное решение
соответствует комплексное решение
 ,
,
которое, очевидно, может быть записано в виде
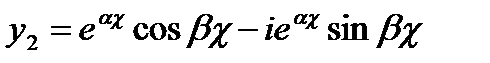
То есть является линейной комбинацией тех же действительных решений (13.13). Таким образом, мы можем сказать, что паре сопряженных комплексных корней характеристического уравнения (13.6) соответствует два действительных частных решения уравнения (13.1) вида (13.13).
Заметим, что в случае п=2, общее решение уравнения 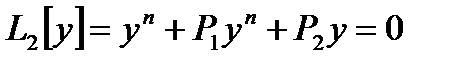 , когда F (к)=к2 + Р1к + Р2 =0 имеет комплексные корни
, когда F (к)=к2 + Р1к + Р2 =0 имеет комплексные корни 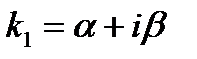 ,
, 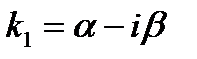 записывается в виде
записывается в виде
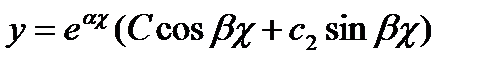
Пример 13.3: Уравнению у" + у’= 0 соответствует характеристическое уравнение k2+1 = 0 и комплексные корни k1=i, k 2=-i, сопряженные друг другу. В соответствующей форме решение имеет вид:
Используя формулы Эйлера, общее решение можно записать
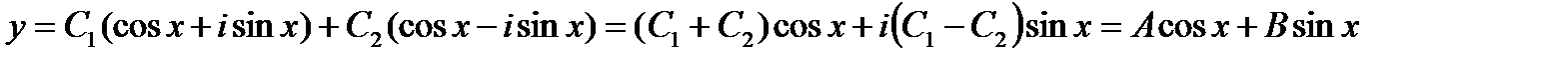
Здесь А и В произвольные постоянные, поэтому уравнения А=С1+С2, В=i(С1-C2) могут быть решены относительно С1,C2, при любых А,В.
Пример 13.4: Уравнение у" + у' = 0 при любых А, В характеристическое уравнение k2 +k-1 = 0 с корнями
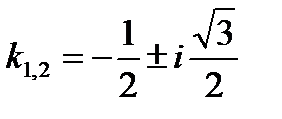
общее решение уравнения запишется в виде
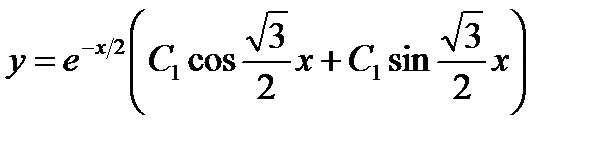
Пример 13.5: Уравнение свободного гармонического колебания
имеет вид
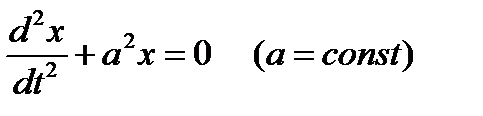
Следовательно, характеристическое уравнение будет к2+а2=0, а его корни будут к = ±ai. Отсюда находим, что частные комплексные решения будут иметь вид х1=еiatх1=е-iat, в то время как частные решения действительные будут x1=cosat, x2=sinat. Общее решение
х0 = С1cos аt + С2 sinаt
Введем постоянные А и  , связанные с С1 и С2 соотношениями:
, связанные с С1 и С2 соотношениями:
С1=А  , С2 =А
, С2 =А 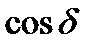
А и 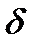 однозначно определяется, если А>0,
однозначно определяется, если А>0, 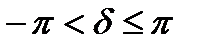 .
.
Тогда решение представляется в виде Х=Аsin(аt+ 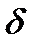 ) Геометрически ясно, что интегральные кривые в плоскости хоt представляют семейство синусоидов. Заданное в уравнении постоянное, а называется частотой колебания. Период колебания Т получается при возрастании аргумента sin на 2
) Геометрически ясно, что интегральные кривые в плоскости хоt представляют семейство синусоидов. Заданное в уравнении постоянное, а называется частотой колебания. Период колебания Т получается при возрастании аргумента sin на 2 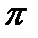 , то есть при возрастании t на
, то есть при возрастании t на 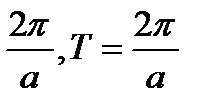 . Число колебаний, в единицу времени
. Число колебаний, в единицу времени 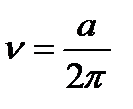 , оно отличается от частоты множителем
, оно отличается от частоты множителем 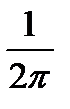 .
.
Постоянная интеграция А характеризует наибольшее по абсолютной величине значение функции х - амплитуду колебаний, наконец, постоянная 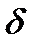 есть начальная фаза.
есть начальная фаза.
3. Пусть корни характеристического уравнения (13.6) кратные.Для простоты обсуждения рассмотрим линейное однородное уравнение второго порядка с постоянными коэффициентами
у' + py' + qy = 0, (13.14)
Где р,q=const
В этом случае характеристическое уравнение имеет вид
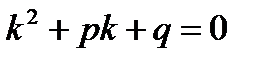 и
и 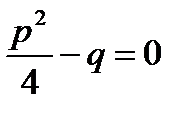 (13.15)
(13.15)
Тогда
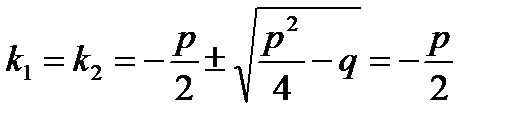
Поэтому одно частное решение уравнения (13.1) будет у1 = ек,х Если всякое другое решение у2 будем искать в виде у2 = 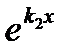 то у1,у2 линейного зависимы, то есть определитель Вронского равен нулю. Таким образом, всякое другое частное решение у2, линейно независимое с у1, будем искать в виде
то у1,у2 линейного зависимы, то есть определитель Вронского равен нулю. Таким образом, всякое другое частное решение у2, линейно независимое с у1, будем искать в виде
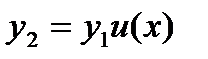 (13.16)
(13.16)
где u(х) неизвестная функция. Дифференцируя функцию (13.16), находим
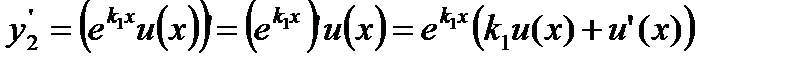
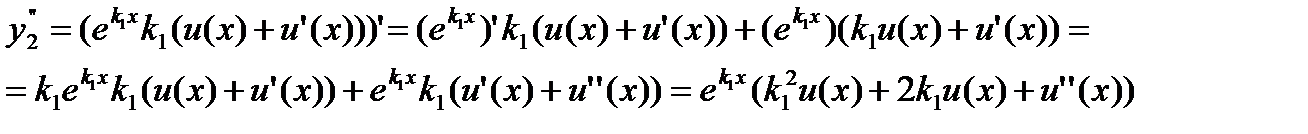
Подставляя у2,y'2,у''2 в уравнение (13.14), после сокращения на общий
множитель 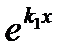 получим
получим
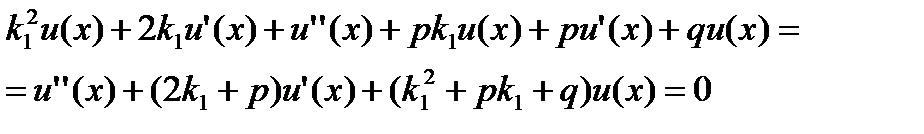
Так как к1 является корнем характеристического уравнения к2+рк+q=0, то к12 + рк1+q = 0, и в силу кратности корня
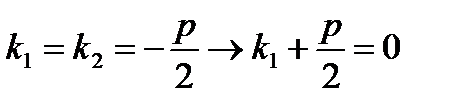 или 2k1+ р = 0, тогда мы получим
или 2k1+ р = 0, тогда мы получим
и"(х)=0 ( )
)
Откуда
и(х)=А, и(х)=Ах+В,
где А и В -произвольные постоянные.
Следовательно,
у2(х)=(Ах + В)хек1x:
Так как мы интересуемся только частными решениями, то можно принять А=1 В=0. Тогда
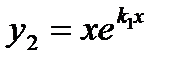
В этом случае у1,y2 линейно независимы. Действительно,
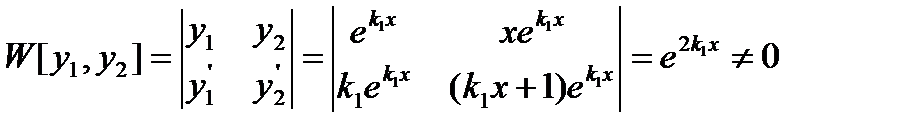
Что доказывает линейно независимость функции у1. у2.
Таким образом, общее решение уравнения (13.14) в случае (3) будет
у = (С1х+Сгх) 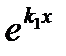 (13.17)
(13.17)
Замечание:
Если характеристическое уравнение (13.6)
имеет корень к, кратности m1, корень к2, кратности m2… корень kj кратности mj что 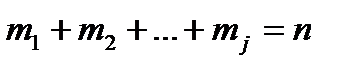 m, то общее решение уравнения (13.1) имеет вид
m, то общее решение уравнения (13.1) имеет вид
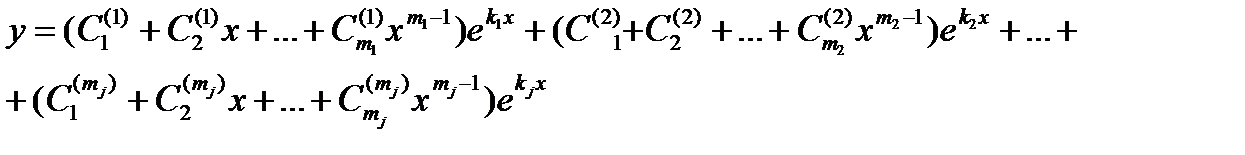
Пример 13.6: Пусть у" - 6у' + у = 0
Решая характеристическое уравнение k2 -6k + 9 = 0
Находим кратный корень к1,2 = 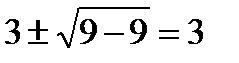 .
.
Следовательно, общее решение запишется в виде у = е3x*(с1+с2х)
Составим таблицу-общего вида решений однородного уравнения 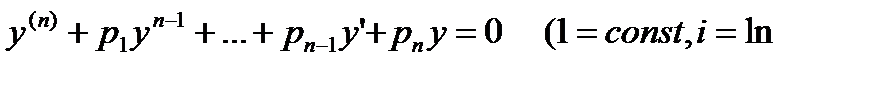 в зависимости от корней характеристического уравнения
в зависимости от корней характеристического уравнения
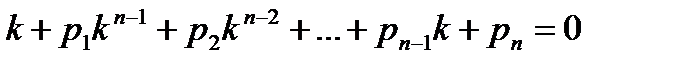
| № п/п | Характер корней характеристического уравнения | Вид общего решения |
| Корни k1,k2,..kn, действительные и различные | 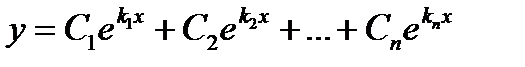 | |
Корни 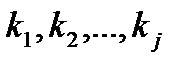 имеют кратности имеют кратности 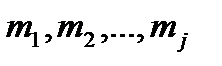 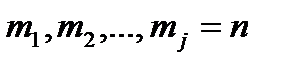 | 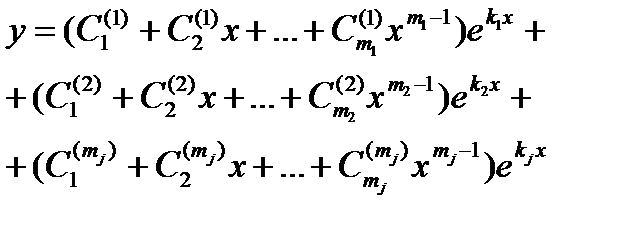 | |
Корни комплексные 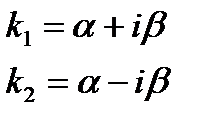 | 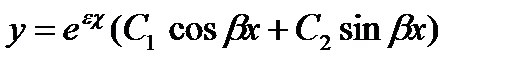 |
 2015-03-07
2015-03-07 1369
1369