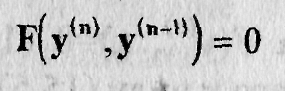Уравнение вида

(11.11)

Уравнение вида (11.11) приводится к квадратурам при любом

натуральном n.

Предположим, что (11.11)разрешено относительно у⁽ⁿ⁾

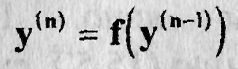(11.11')

Вводим новую функцию х, z = y^(n-1), уравнение примет вид

z' = f(_Z)

Из этого уравнения получаем с помощью разделения переменных общий интеграл

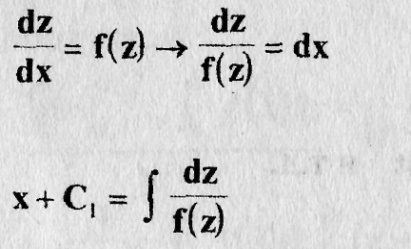
Допустим, что соотношение разрешено относительно z:

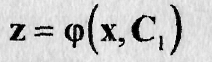
Заменяя z eгo значением y^(n-1), получим уравнение (n-і)-го порядка

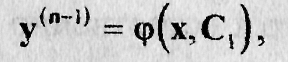
которое мы рассмотрели в пункте A

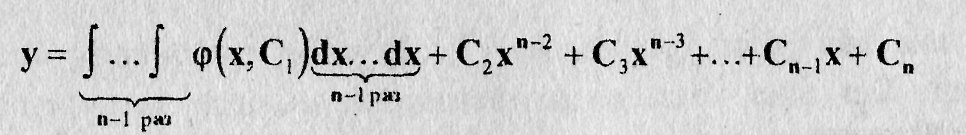
Если уравнение (11.11) неразрешено в элементарных функциях относительно у^(п), но мы имеем выражения y^(n-1), и y^(n-1), через параметр

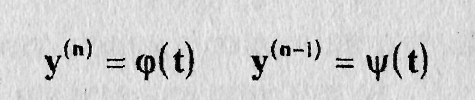(11.11")

to соотношение dy' ' = y dx или 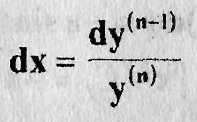дает нам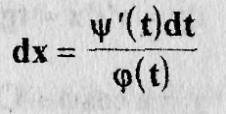

Откуда х получается квадратурой

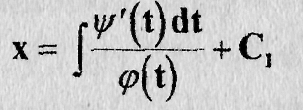
Далее, находим последовательно

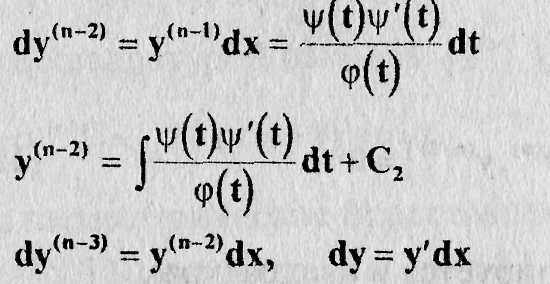
и наконец

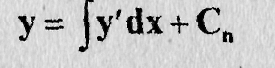
To есть опять представление у и х в функции параметра t и п произвольных постоянных N₁, N₂,...,N_n, следовательно, общее решение

Пример 11.5:

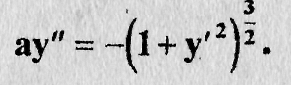Согласно изложенной теории, полагая y=z,

получаем уравнение первого порядка

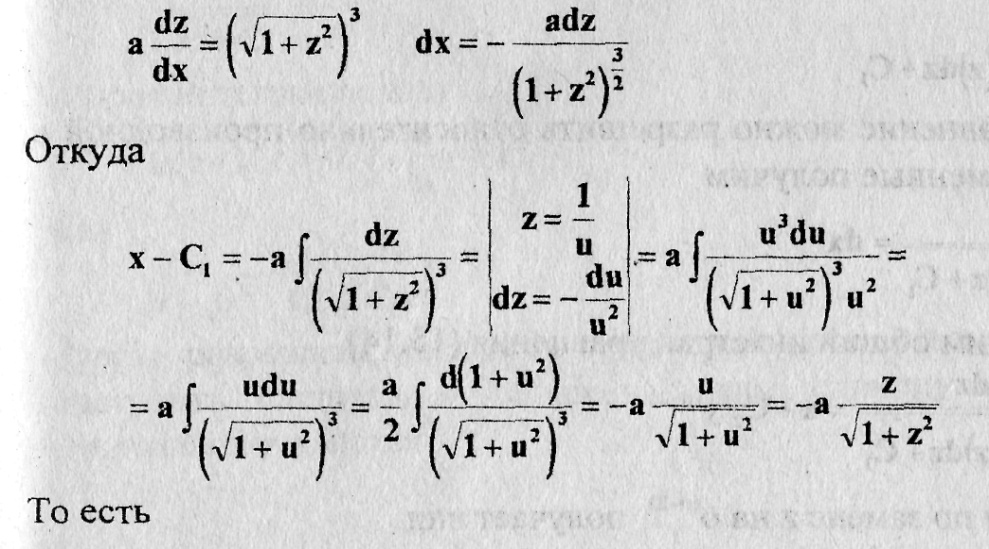
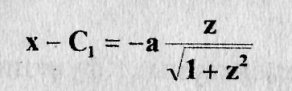
Дальше удобно интегрировать в параметрическом виде

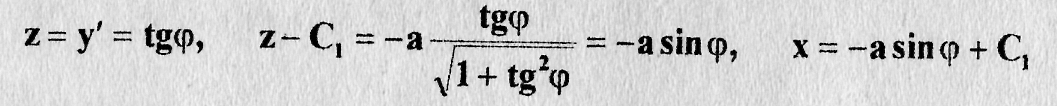
Откуда находим

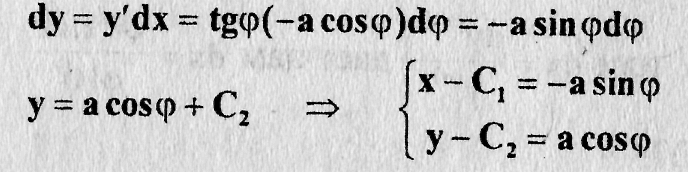
исключая параметр 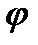, имеем

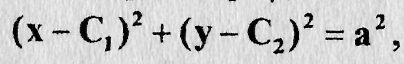
представляющее уравнение семейства всех окружностей радиуса а на \ плоскости.