Пусть уравнение n-го порядка не содержит явно искомой у, для общности предположим, что оно не содержит ее к-1 первых производных у ',у″,…. У(k-1) и низшая производная, явно входящая в уравнение, есть
У(k) (1≤к≤n-1)
Уравнение имеет вид:
F(х, у(k),(k+1), …у(n))=0 (12.4)
Полагая у(k) =z, мы заменяем уравнение (12.4) уравнением
F(х, z, z', z(n-k))=0 (12.4')
Порядка n-к. Противоположность случаем,рассмотренным в лекции 11 здесь мы не можем утверждать что уравнение (12.4') всегда интегрируется в квадратурах. Но вместо уравнения n-го порядка мы получили уравнение порядка n-к< n. Допустим что сумели найти общий интеграл уравнения (12.4')
Φ(x, z, С1, С2, …,С п -к)=0 (12.5)
Уравнения (12.5) есть промежуточный интеграл уравнения (12.4), содержащий n-к постоянных. Само уравнение (12.5) принадлежит к типу (12.5'), то есть заведомо интегрируется в квадратурах, и, решая. его найдем общий интеграл уравнения (12.4). Если к=n, мы непосредственно имеем уже рассмотренное нами уравнения. Рассмотрим частный уравнения (12.4), то есть уравнение вида
y″= f (x,y') (12.6)
или
F (x, y',y″)=0 (12.6')
Пологая y'= z, y″= z' и подставляя в (12.6) мы получим уравнение первого порядка
Z'= f (x, z)
или
dz / dx f(x,z)
Отсюда
Z= P(x,C1)
Учитывая, что z=y', получим общий интеграл уравнения (12.6)
Y= ∫P(x,C1)dx+C2 (12.7)
Пример 12.2:Найти частное решение уравнения
xy″+y'+x=0 (12.8)
Удовлетворяющее условиям
y │x=1=0,y'│x=1=0 (12.9)
Решение: Пологая y'=z,y″=z', получим
xz'+z+x=0
Таким образом, мы получили линейное уравнение первого порядка, которое в силу формулы (9.16,лек.9)
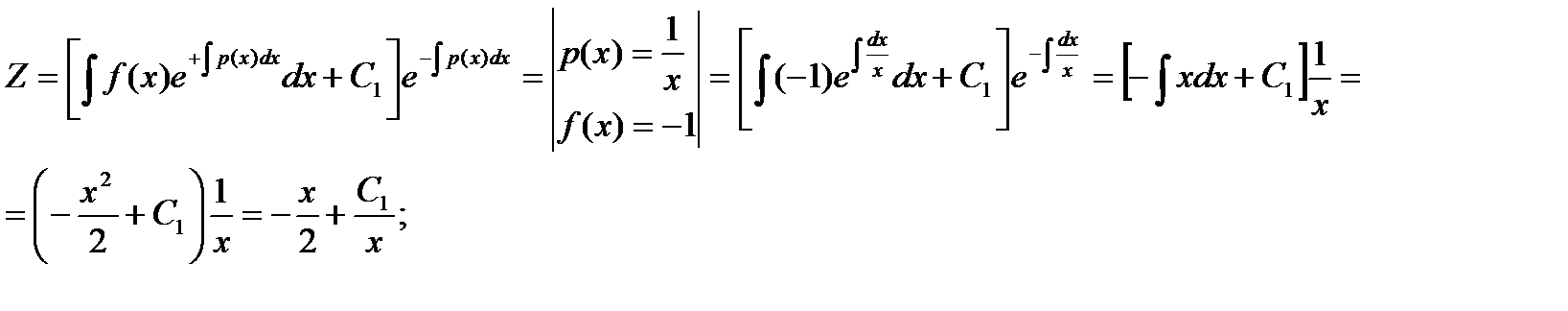
Так как z=y' то имеем
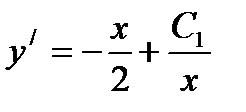 (y(n)=f(x)) (12.10)
(y(n)=f(x)) (12.10)
Полученное уравнение является частным случаем уравнения (12.6) при n=1. Тогда
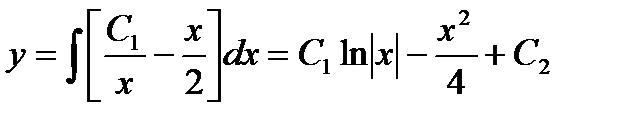
Определим частное решение из условия (12.9)
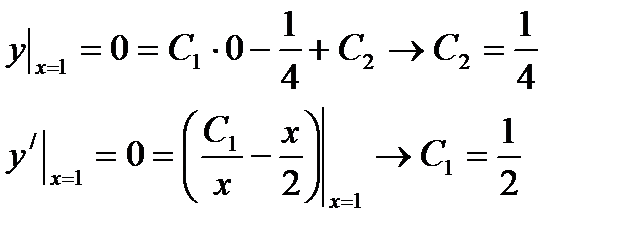
Таким образом, решение уравнения (12.8)-(12.9) имеет вид
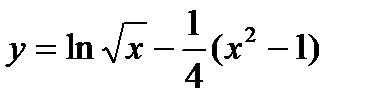
Примеры 12.3: Найти общее решение уравнения
x²y″y'²=0 или y″=(y'/x)² (12.6)
F(x,y',y″)=0 y″=f(x,y) (12.6')
Решение: пологая, у=z, y″=z' подставляя в уравнение, имеем
x²zz²=0 или 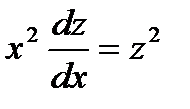
Полученное уравнение первого порядка является уравнением с разделяющимся переменными. Разделив переменные, получим
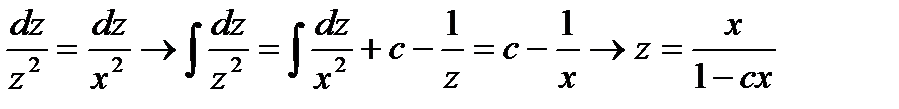
Учитывая что z=у, получим
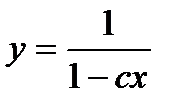
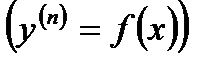 (12.10)
(12.10)
Отсюда
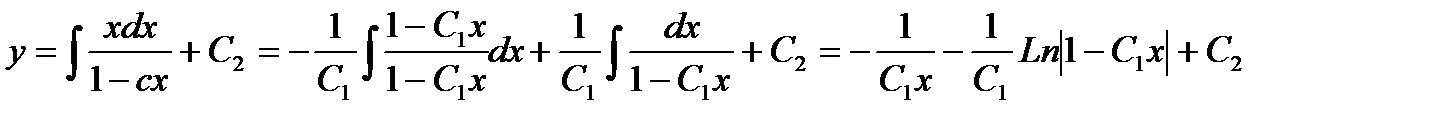
Ответ: 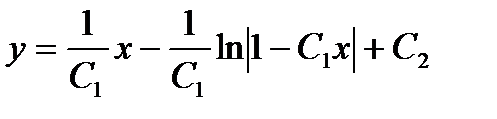
 2015-03-07
2015-03-07 572
572








