2015-03-07
1158
Пусть члены ряда (16.1) положительны и не возрастают, то есть:
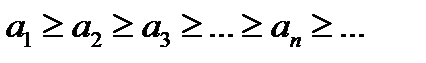
И пусть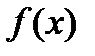 
-такая непрерывная невозрастающая функция, что
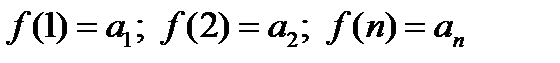(16.11)
Тогда справедливы следующие утверждения:
1) если несобственный интеграл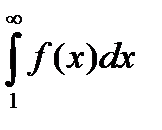 
сходится, то сходится и ряд (16.1)
2) если указанный интеграл расходится, то и расходится ряд (16.1)
Доказательство:
Изобразим члены ряда геометрически, откладывая по оси абсцисс номера 1,2,3,…,n.n+1… членов ряда, а по оси ординат соответствующие значения членов ряда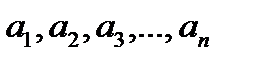 
. Построим на том же чертеже график непрерывно не возрастающей функции 
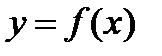, удовлетворяющий условию (16.11)
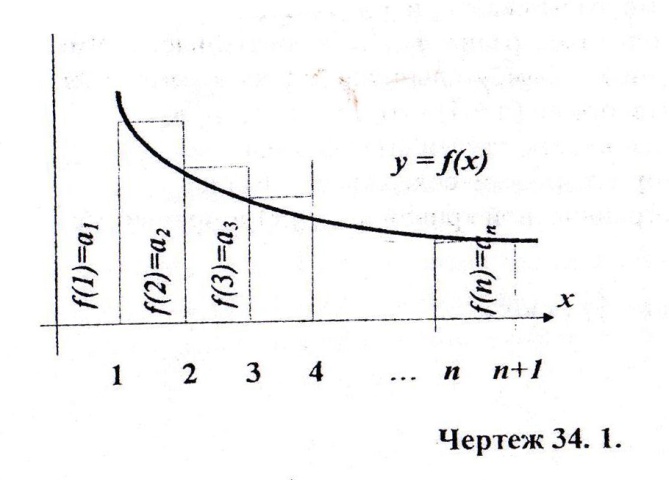
Из чертежа видно что первый из построенных прямоугольников имеет основание 1 и высоту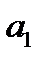 
. Следовательно, площадь этого прямоугольника 
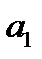. Площадь второго прямоугольника 
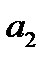и т.д. наконец, площадь последнего (n-го) из построенных 
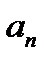. Сумма площадей построенных прямоугольников равна сумме 
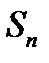первых n членов ряда. С другой стороны, ступенчатая фигура, образованная этими прямоугольниками заключает область, ограниченную кривой 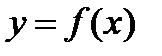и прямыми х=1, х=n+1, у=0. площадь этой области равна
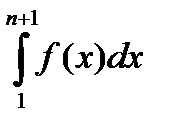
Следовательно:
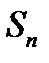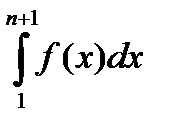> (16.12)
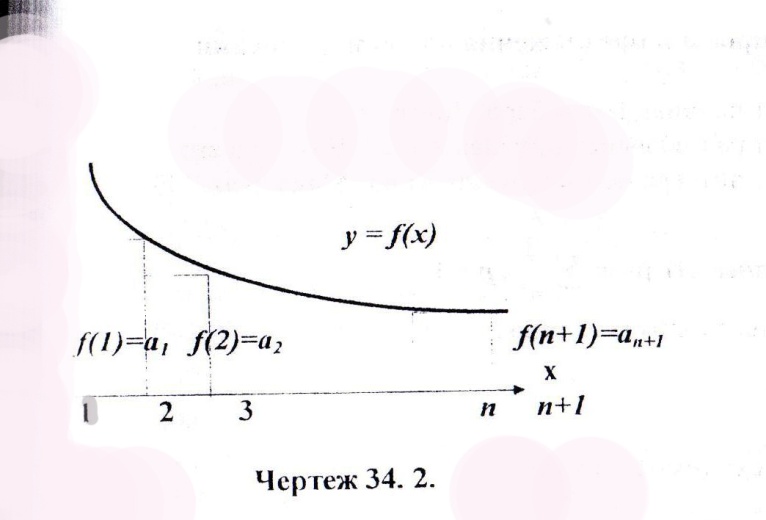
Рассмотрим чертеж 2. здесь первый (слева) из построенных прямоугольников имеет высоту 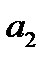, следовательно его площадь также 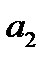. Площадь второго 
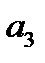и т.д площадь последнего из построенных прямоугольников равна сумме всех членов ряда, начиная от второго до (n+1)-го, то есть 
.
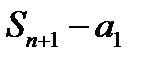С другой стороны, как легко видеть, ступенчатая фигура, образованная этими прямоугольниками, содержится внутри криволинейной фигуры, ограниченной кривой 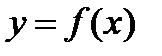и прямыми х=1, х=n+1, у=0.
Площадь этой фигуры равна 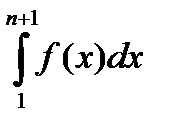, следовательно,
<
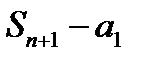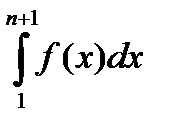
Откуда
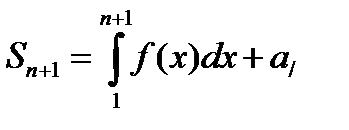(16.13)
Рассмотрим оба случая.
1. Предположим что интеграл 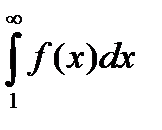сходится, то есть имеет конечное значение. Так как
< ,
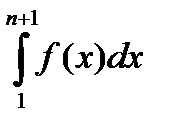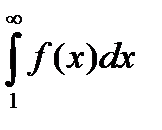то в силу (34.13)
,
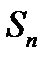
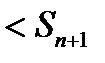
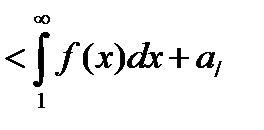То есть частичная сумма остается ограниченной при всех значениях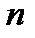 
. Но при увеличении 
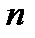она возрастает, так как все члены 
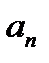положительны. Следовательно, 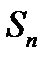при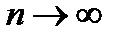 
имеет конечный предел 
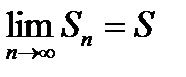, то есть ряд сходится.
2. Предположим далее, что
= 
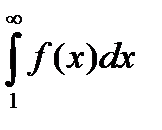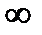
Это означает, что 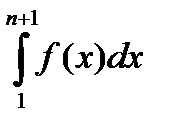неограниченно возрастает при возрастании 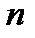. Но тогда в силу неравенства (16.13) 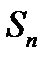также неограниченно возрастает при возрастании 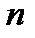, то сть ряд расходится.
