2015-03-07
363
Применим интегральный признак, положив
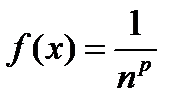
Эта функция удовлетворяет всем условиям теоремы.
Рассмотрим интеграл
При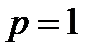 
|
При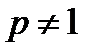 
|
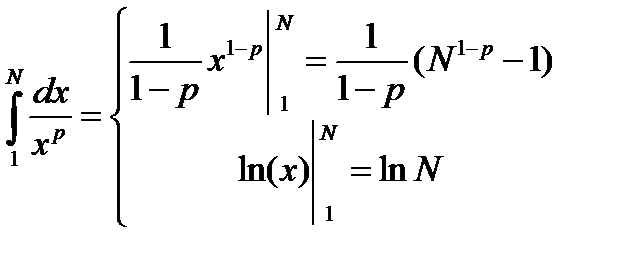
По определению несобственного интеграла, имеем:
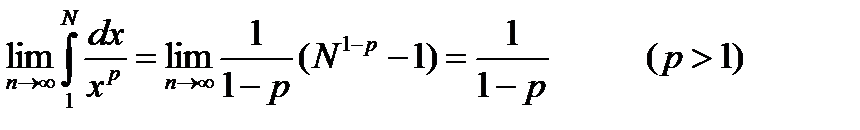
И несобственный интеграл сходится и, следовательно, данный ряд также сходится
,
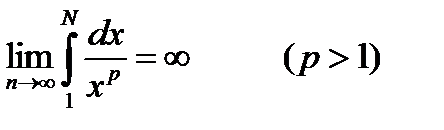Следовательно, несобственный интеграл расходится, и ряд будет расходящимся.
