Рассмотрим сумму 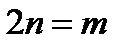 первых членов ряда (17.1)
первых членов ряда (17.1)
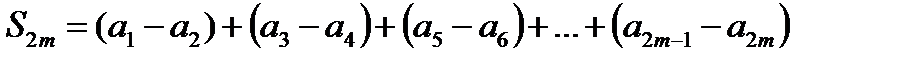
Из условия (17.3) следует, что выражение в каждой скобке положительно. Следовательно сумма 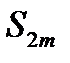 положительна и возрастает с возрастанием
положительна и возрастает с возрастанием 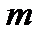 .
.
Запишем теперь эту сумму так:
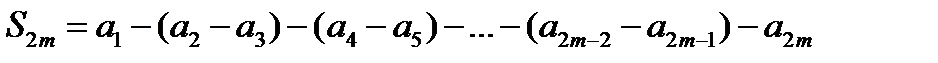
В силу условия (17.3) каждая скобка положительна. Поэтому в результате вычитания этих скобок из 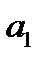 мы получим число меньше чем
мы получим число меньше чем 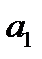 , то есть
, то есть 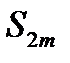
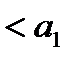 .
.
Таким образом мы установили, что 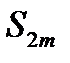 при возрастании
при возрастании 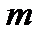 возрастает и ограничена сверху. Отсюда следует что
возрастает и ограничена сверху. Отсюда следует что 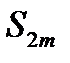 имеет предел
имеет предел  :
:
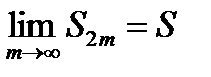 ,
,
причем: 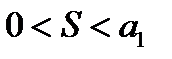
однако сходимость ряда еще не доказана.
Мы доказали только, что последовательность имеет пределом число  . Докажем теперь, что нечетные частичные суммы также стремятся к пределу
. Докажем теперь, что нечетные частичные суммы также стремятся к пределу  .
.
Рассмотрим для этого сумму 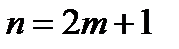 первых членов ряда (17.1).
первых членов ряда (17.1).
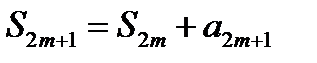
Так как по условию (17.2) 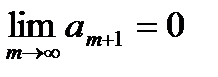 , то следовательно,
, то следовательно,
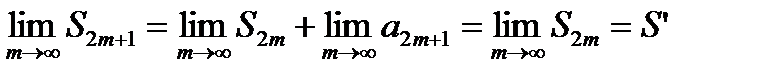
Тем самым мы доказали что, 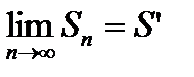 , как при четном
, как при четном 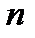 , так и при нечетном
, так и при нечетном 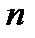 . Следовательно ряд (17.1) сходится.
. Следовательно ряд (17.1) сходится.
Пример 17.1 Знакочередующийся ряд
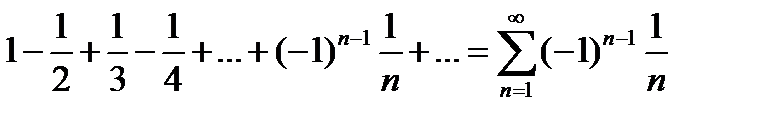
 2015-03-07
2015-03-07 366
366








