Решение. Согласно теореме (17.1) имеем

Согласно теореме (17.1) имеем:

a)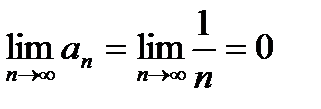

b)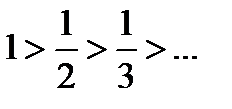

c) Следовательно ряд сходится.

Следствие: для знакочередующегося ряда (17.1) при всех 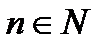справедливы неравенства:

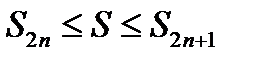
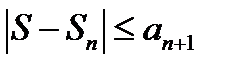
§ 2. Знакопеременные ряды.Абсолютная и условная сходимости.

Ряд называется знакопеременным, если среди его членов имеются как положительные, так и отрицательные. Нетрудно заметить, что знакочередующиеся ряды являются частным случаем знакопеременных рядов.