Пусть 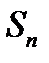 и
и 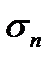 сумма
сумма 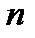 первых членов ряда (17.4) и (17.5). далее пусть
первых членов ряда (17.4) и (17.5). далее пусть 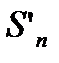 -сумма всех положительных, а
-сумма всех положительных, а 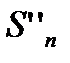 -сумма абсолютных величин всех отрицательных членов среди первых
-сумма абсолютных величин всех отрицательных членов среди первых 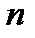 членов данного ряда. Тогда:
членов данного ряда. Тогда:
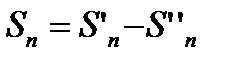 ;
; 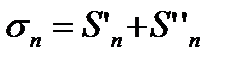
По условию 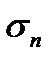 имеет предел
имеет предел  ;
; 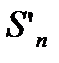 и
и 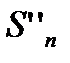 -положительные возрастающие величины меньше
-положительные возрастающие величины меньше  . Следовательно они имеют и этот предел равный
. Следовательно они имеют и этот предел равный 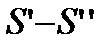 , то есть знакопеременный ряд (17.4) сходится.
, то есть знакопеременный ряд (17.4) сходится.
Пример 17.4. Исследовать сходимость ряда
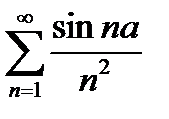 (17.6)
(17.6)
Решение. Наряду с данным рядом, рассмотрим ряды
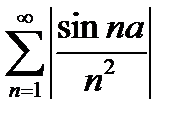 (17.7)
(17.7)
и 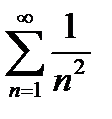 (17.8)
(17.8)
Ряд (17.8), сходится. Члены ряда (17.7)не больше соответствующих членов ряда (17.8), следовательно, ряд (17.6) тоже сходится.
Применяя критерий Коши сходимости ряда к ряду (17.5), получим:
Для того чтобы ряд (17.5) абсолютно сходился необходимо и достаточно, чтобы 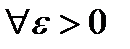 существовал такой номер
существовал такой номер 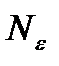 , чтобы для всех
, чтобы для всех 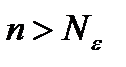 , и всех целых
, и всех целых 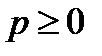 выполнялось неравенство:
выполнялось неравенство:
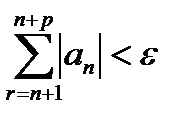
 2015-03-07
2015-03-07 446
446








