Если ряд сходится абсолютно, то он остается абсолютно сходящимся при любой перестановки его членов.
Свойство 17.1 Если ряд абсолютно сходится, то он сходится просто.
Доказательство. Пусть ряд (17.5) сходится. Тогда для него выполняется условие Коши, то есть:
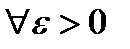
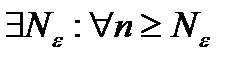
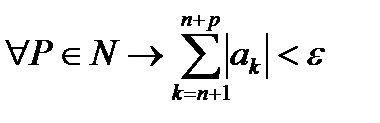
Так как 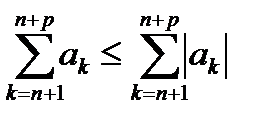 , то и для ряда (17.4) выполняется условие Коши, и в силу критерия Коши этот ряд сходится.
, то и для ряда (17.4) выполняется условие Коши, и в силу критерия Коши этот ряд сходится.
Свойство 17.2 Если ряд (17.4) абсолютно сходится, а последовательность 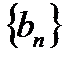 ограниченная, то есть
ограниченная, то есть
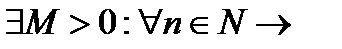
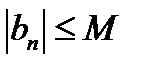 , (17.9)
, (17.9)
То ряд 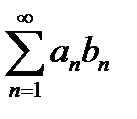 абсолютно сходится.
абсолютно сходится.
Доказательство. Для доказательства свойства 17.2 следует воспользоваться критерием Коши сходимости ряда и неравенством:
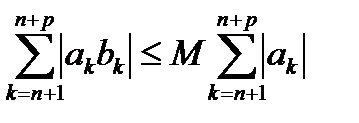 ,
,
которое выполняется в силу условия (17.9).
Свойство 17.3. Если ряды 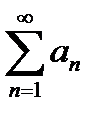 и
и 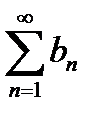 абсолютно сходятся, то при любых
абсолютно сходятся, то при любых 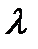 и
и 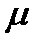 абсолютно сходится ряд
абсолютно сходится ряд
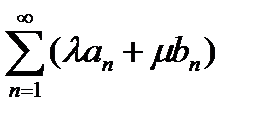
Свойство 17.4. Если ряды 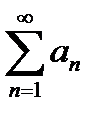 и
и 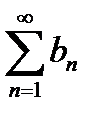 абсолютно сходятся, то и ряд
абсолютно сходятся, то и ряд
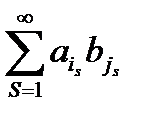 (17.10)
(17.10)
составленный из всевозможных попарных произведений членов рядов (17.4) и (17.10), абсолютно сходится, причем сумма рядов равна произведению сумм рядов (17.4) и (17.10).
Свойства 17.5. Если ряд 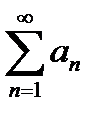 , абсолютно сходятся, то ряд
, абсолютно сходятся, то ряд 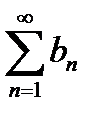 и
и 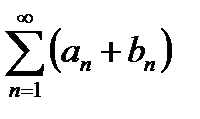 одновременно либо абсолютно сходится, либо условно сходится либо расходится.
одновременно либо абсолютно сходится, либо условно сходится либо расходится.
Теорема 17.4. Теорема Римана. Если ряд (17.4) условно сходится, то каково бы ни было число 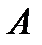 можно так переставить члены ряда, что сумма ряда станет равной
можно так переставить члены ряда, что сумма ряда станет равной 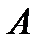 .
.
 2015-03-07
2015-03-07 1199
1199
