Примеры. I.Найти радиус сходимости ряда

I. Найти радиус сходимости ряда

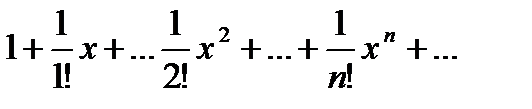
Имеем:

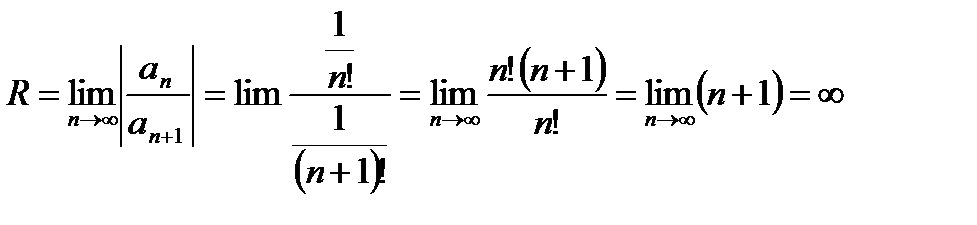
Следовательно, ряд сходится при всех значениях х, то есть R=.

В силу необходимого признака сходимости, общий член рассматриваемого ряда стремится к нулю

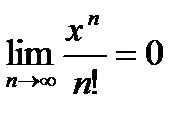
при любых х. Это замечание будет существенным образом использовано в дальнейшем.

2. Найти радиус сходимости ряда

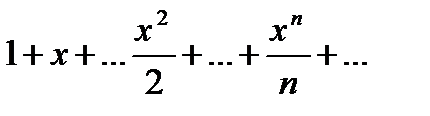
Имеем:

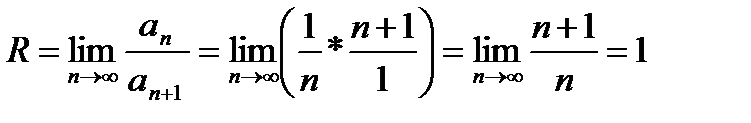
Радиус сходимости ряда R=1. Рассмотрим поведение ряда на концах интервала сходимости. При х=1 получаем расходящийся ряд:

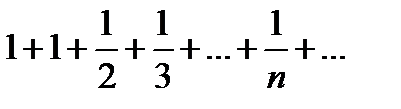
а при x=-1 ряд:

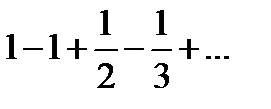
сходящийся не абсолютно.

3. Исследовать ряд

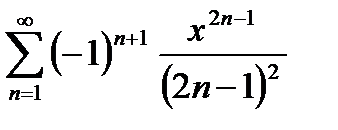
Решение:

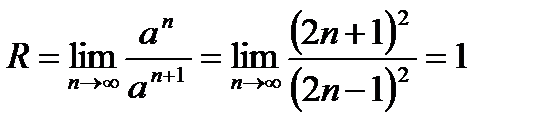
ряд сходится при 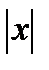< 1 и расходится при 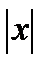>1.

4. Найти интервал сходимости ряда

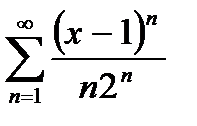
Имеем:

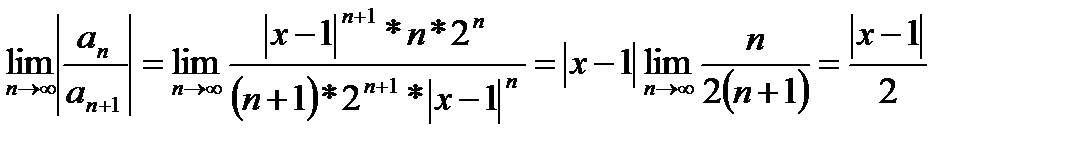
Ряд сходится, если 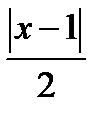<1, то есть -2<х-1<2. Таким образом,

интервал сходимости ряда является интервал (1,3) с центром в точке х=1

' §4. Общие свойства степенного ряда

Рассмотрим степенной ряд (19.2), имеющий радиус сходимости R (R может равняться ∞).

В интервале сходимости ряда его сумма является некоторой функцией f(x). (говорят, что ряд сходимости к f(x) или что он представляет функцию f(x)).

Сформулируем в виде теорем общие свойства степенных рядов, доказывать эти теоремы мы не будем.

Теорема 19.3. Сумма степенного ряда (19.2) есть функция непрерывная в интервале сходимости ряда.

Теорема 19.4. Степенной ряд, полученный в результате почленного интегрирования ряда (19.2) в интервале [0,х], сходится для — R<x<R к соответствующему интегралу от суммы f(x) ряда (19.2).

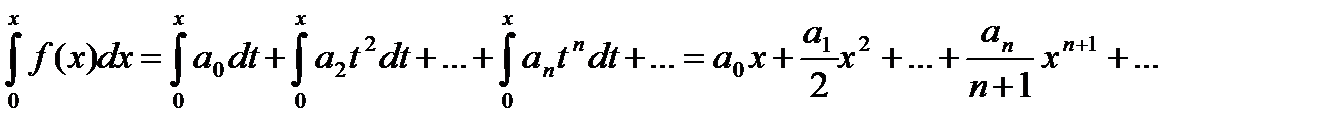
-R<x<R

Теорема 19.5. Степенной ряд в интервале его сходимости можно, дифференцировать почленно, так что:

f’(x)=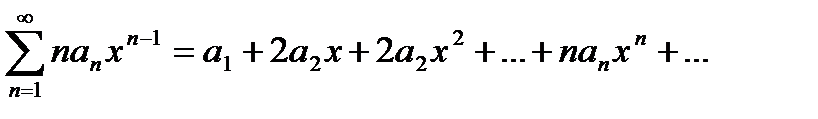

Замечание. Степенной ряд в интервале его сходимости можно почленно дифференцировать любое число раз.