Тема: Ряд Тейлора для функции  .. Ряды Тейлора и Маклорена. Достаточные условия представимости функции рядом Тейлора.Примеры разложения основных элементарных функций в ряд Тейлора.
.. Ряды Тейлора и Маклорена. Достаточные условия представимости функции рядом Тейлора.Примеры разложения основных элементарных функций в ряд Тейлора.
§1. Ряд Тейлора для функции 
1.Определение ряда Тейлора. Пусть  при х=а имеет конечные производные
при х=а имеет конечные производные 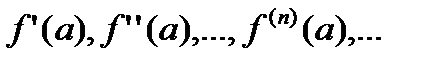 , то есть
, то есть 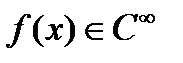 в точке
в точке 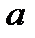 . Тогда рядом Тейлора функции
. Тогда рядом Тейлора функции 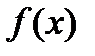 относительно точки
относительно точки 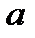 называют ряд:
называют ряд:
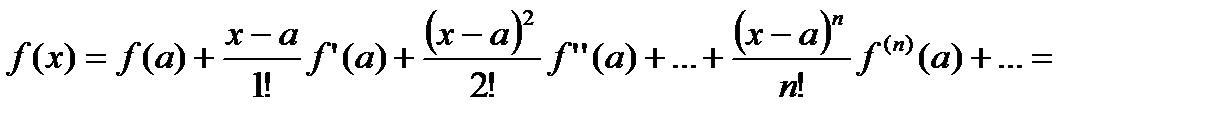
= 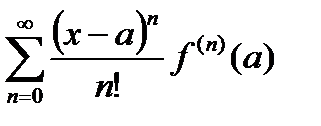 (20.1)
(20.1)
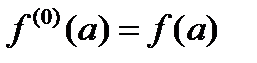 ; 0!=1
; 0!=1
Если для некоторой функции  составлен ряд Тейлора, то говорят что
составлен ряд Тейлора, то говорят что  разложена в ряд Тейлора.
разложена в ряд Тейлора.
2. Теорема единственности. Пусть ряд Тейлора для некоторой функции  сходится в интервале
сходится в интервале 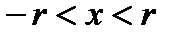 и пусть его сумма равна
и пусть его сумма равна 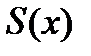 .
.
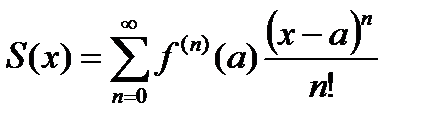
Теорема 20.1(единственности). Если в некоторой окрестности точки 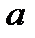 функция
функция  равна сумме степенного ряда:
равна сумме степенного ряда:
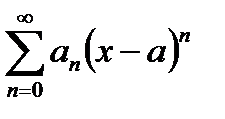 ,
,
то этот ряд есть ее ряд Тейлора в окрестности точки 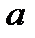 .
.
 2015-03-07
2015-03-07 415
415








