Так как степенной ряд можно почленно дифференцировать, то получаем
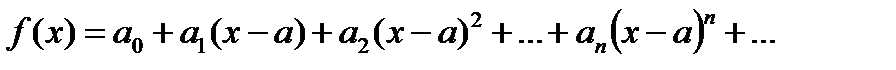
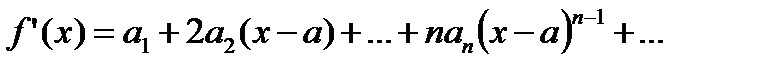
……………………………………………………
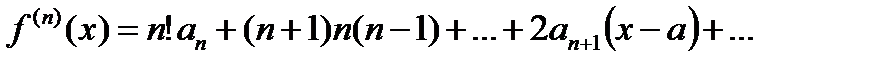
Пологая в этих равенствах х=а, будем иметь:
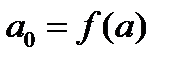 ,
, 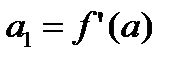 , …,
, …, 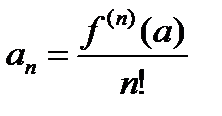 …
…
и значит, теорема доказана.
Следствие 20.1. Если сумма степенного ряда тождественно равна нулю:
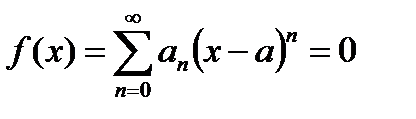 ,
,
то все его коэффициенты равны нулю.
Действительно, Так как 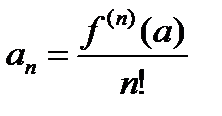 , а
, а 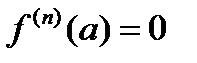 , то
, то 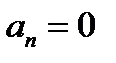 при любом
при любом 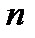 .
.
Из установленного следствия в свою очередь вытекает
Теорема 20.2. Функция 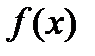 в окрестности одной и той же точке
в окрестности одной и той же точке 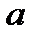 не имеет различных представлений в виде степенного ряда по степеням
не имеет различных представлений в виде степенного ряда по степеням 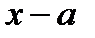 .
.
В самом деле, предположим, что 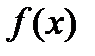 в окрестности точки
в окрестности точки 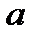 , представляя двумя степенными рядами:
, представляя двумя степенными рядами:
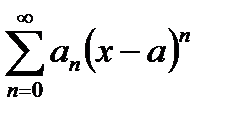
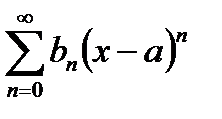
Тогда вычитая второе неравенство из первого, получим:
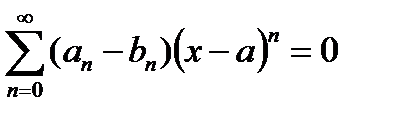
И значит в силу следствия 20.1, 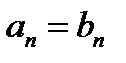
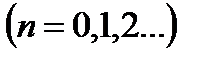
Из доказанной теоремы вытекает следующее.
Определение 20.1. Рядом Тейлора функции 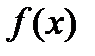 в окрестности точки
в окрестности точки 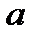 называется степенной ряд (20.1) относительно разности
называется степенной ряд (20.1) относительно разности 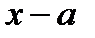 , коэффициенты которого
, коэффициенты которого 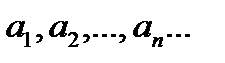 выражаются через функцию
выражаются через функцию 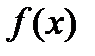 и ее производные в точке а по формуле:
и ее производные в точке а по формуле:
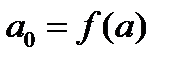 ,
, 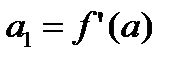 , …,
, …, 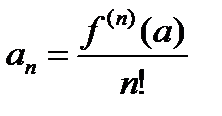 …
…
Эти коэффициенты называются коэффициентами Тейлора функции 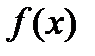 в точке
в точке 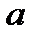 .
.
3. Представление функции 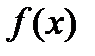 ее рядом Тейлора.
ее рядом Тейлора.
Из теоремы существования следует, что если 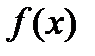 вообще представима степенным рядом, то она представима своим рядом Тейлора, то есть в этом случае ряд Тейлора, составленный для функции
вообще представима степенным рядом, то она представима своим рядом Тейлора, то есть в этом случае ряд Тейлора, составленный для функции 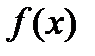 , сходится к ней самой.
, сходится к ней самой.
Пусть некоторая функция 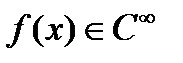 на интервале
на интервале 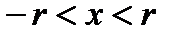 и пусть ее ряд Тейлора сходится на этом же интервале к функции
и пусть ее ряд Тейлора сходится на этом же интервале к функции 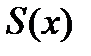 ; естественно спросить: будет ли справедливо равенство
; естественно спросить: будет ли справедливо равенство
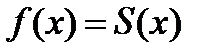 -?
-?
Вообще говоря ответ на этот вопрос отрицательный.
Примером может служить функция:
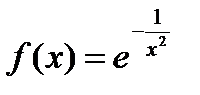 при
при 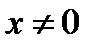 и
и 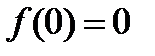
Это –бесконечное число раз дифференцируемая на всей оси ОХ, причем все производные в точке х=0 равны нулю. Действительно,
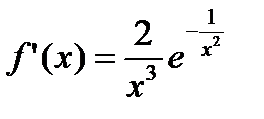 , при
, при  и
и 
Так как
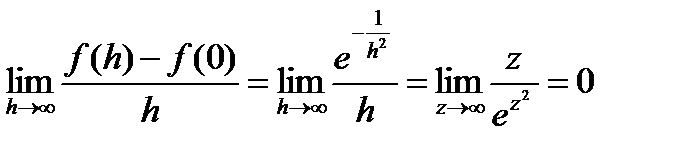
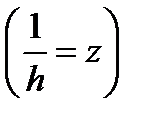
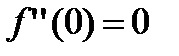 , так как
, так как
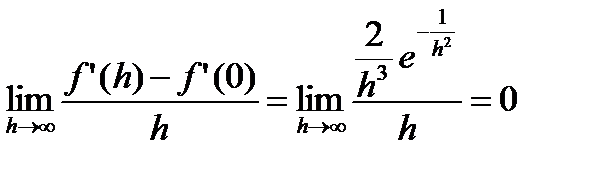
И так далее. Следовательно, все коэффициенты Тейлора функции 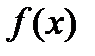 при х=0 равны нулю, и значит, сходится но не к функции
при х=0 равны нулю, и значит, сходится но не к функции 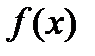 , а к функции тождественно равной нулю.
, а к функции тождественно равной нулю.
Теорема 20.3 Для того чтобы функция 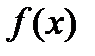 была представлена своим рядом Тейлора относительно точки
была представлена своим рядом Тейлора относительно точки 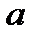 , необходимо и достаточно, чтобы существовали числа
, необходимо и достаточно, чтобы существовали числа 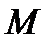 и
и 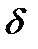 такие, что
такие, что 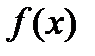 имеет все производные в интервале
имеет все производные в интервале 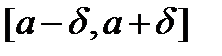 и кроме того, для каждого
и кроме того, для каждого 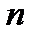 выполняются равенства:
выполняются равенства:
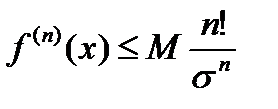
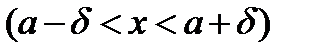
§ 2. Ряды Тейлора и Маклорена
Если 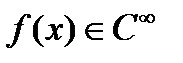 в окрестности точки
в окрестности точки 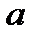 , то как известно из первого курса формула Тейлора имеет вид:
, то как известно из первого курса формула Тейлора имеет вид:
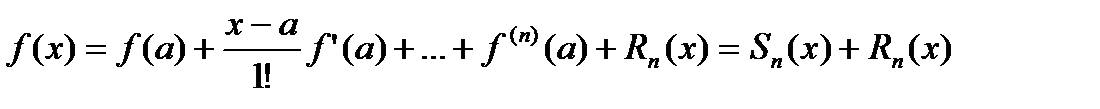 (20.2)
(20.2)
где 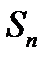 -многочлен
-многочлен 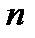 -ой степени, равный сумме первых (
-ой степени, равный сумме первых (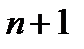 ) членов формулы Тейлора. При
) членов формулы Тейлора. При 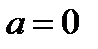 мы получаем формулу Маклорена:
мы получаем формулу Маклорена:
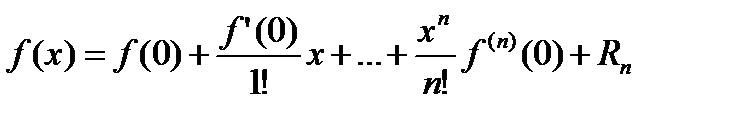 (20.3)
(20.3)
где 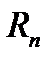 называется остаточным членом
называется остаточным членом
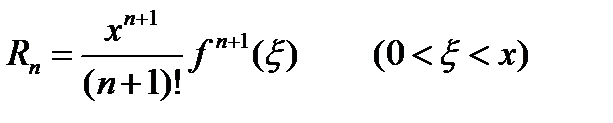 -формула Лагранжа.
-формула Лагранжа.
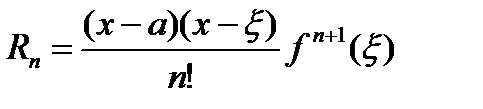 - в форме Коши.
- в форме Коши.
Если функция 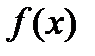 имеет производные всех порядков в окрестности точки а=х, то в формуле Тейлора число
имеет производные всех порядков в окрестности точки а=х, то в формуле Тейлора число 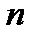 может брать сколь угодно большим. Допустим, что в рассматриваемой окрестности остаточный член
может брать сколь угодно большим. Допустим, что в рассматриваемой окрестности остаточный член 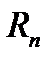 , стремится к нулю при
, стремится к нулю при 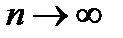
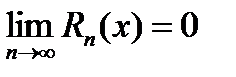
Тогда переходя к формуле (20.2) к пределу при 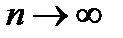 , получим с права бесконечный ряд, который называется рядом Тейлора.
, получим с права бесконечный ряд, который называется рядом Тейлора.
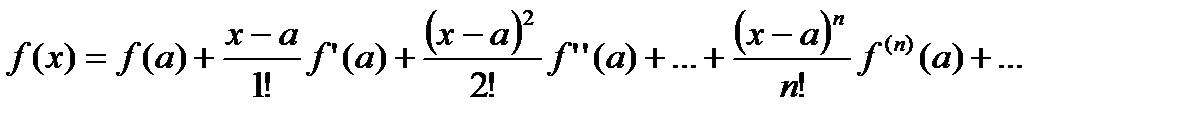 (20.4)
(20.4)
Последнее равенство справедливо лишь в том случае если 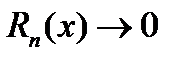 при
при 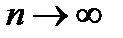 . В этом случае написанный с права ряд сходится и его сумма равна данной функции
. В этом случае написанный с права ряд сходится и его сумма равна данной функции 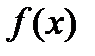
Докажем, что это действительно так.
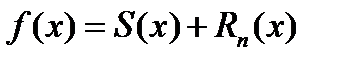 , где
, где 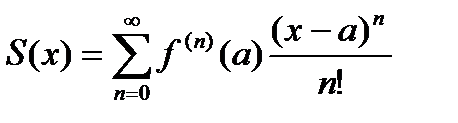
Так как по условию 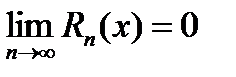 , то:
, то:
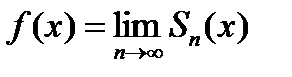 .
.
Но 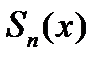 есть
есть 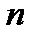 -я частичная сумма ряда (20.1): ее предел равен сумме ряда, стоящего в правой части равенства (20.1).Следовательно (20.1) справедливо.
-я частичная сумма ряда (20.1): ее предел равен сумме ряда, стоящего в правой части равенства (20.1).Следовательно (20.1) справедливо.
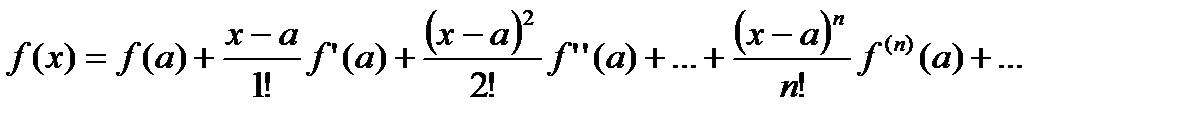 (20.1)
(20.1)
Из предыдущего следует, что ряд Тейлора представляет данную функцию 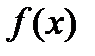 только тогда, когда
только тогда, когда 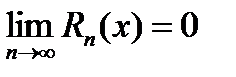
 2015-03-07
2015-03-07 684
684