Пусть 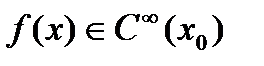 . Тогда ей можно представить в соответствии ряд (20.1). обозначим:
. Тогда ей можно представить в соответствии ряд (20.1). обозначим:
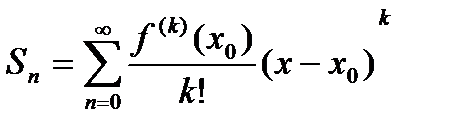 (20.4)
(20.4)
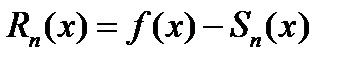 (20.5)
(20.5)
И назовем 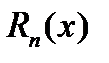 остаточным членом формулы Тейлора для функции
остаточным членом формулы Тейлора для функции  в точке
в точке 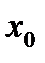 . Если существует
. Если существует
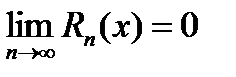 (20.6)
(20.6)
То согласно определению сходимости ряда(20.1), он сходится к функции  в точке
в точке 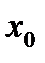 ., то есть
., то есть
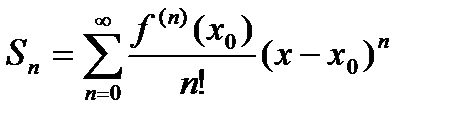 (20.7)
(20.7)
Теорема 20.4 Если функции 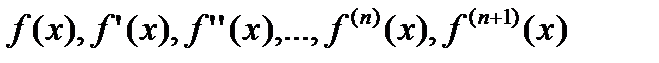 непрерывны на интервале
непрерывны на интервале 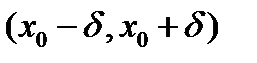 при
при 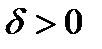 , то для любого
, то для любого 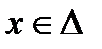 остаточный член формулы Тейлора для функции
остаточный член формулы Тейлора для функции  в точке
в точке 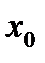 можно представить
можно представить
1. В интегральной форме
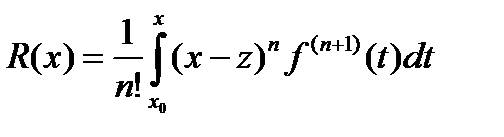 (20.8)
(20.8)
2. В форме Лагранжа
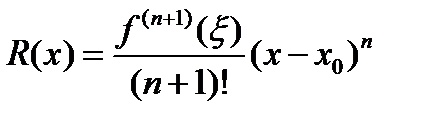 (20.9)
(20.9)
§ 3.Достаточные условия представимости функции рядом Тейлора.
Из полученного выражения для 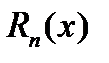 можно в частности, получить такой результат.
можно в частности, получить такой результат.
Теорема 20.5. Если функция  на интервале
на интервале 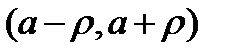 имеет все производные и можно указать число
имеет все производные и можно указать число 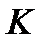 такое что
такое что 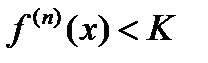 для
для 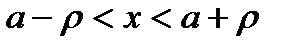 , то
, то  представима рядом Тейлора на этом интервале.
представима рядом Тейлора на этом интервале.
Пусть 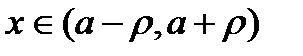 , тогда используя формулу (20.9), и по условию теоремы получаем:
, тогда используя формулу (20.9), и по условию теоремы получаем:
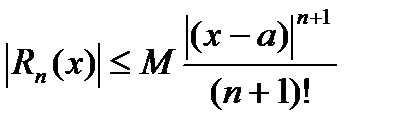 (20.10)
(20.10)
Так как 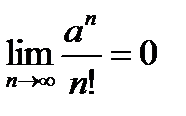 при
при 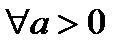 , то из (20.10) следует, что выполняется (20.6), то есть в точке х справедливо равенство (20.7)
, то из (20.10) следует, что выполняется (20.6), то есть в точке х справедливо равенство (20.7)
Теорема 20.6. Для того чтобы функция  была представлена степенным рядом в окрестности точки а достаточно, чтобы существовали числа
была представлена степенным рядом в окрестности точки а достаточно, чтобы существовали числа 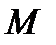 и
и 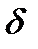 , такие что
, такие что  имеет все производные в интервале
имеет все производные в интервале 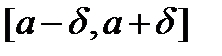 и
и 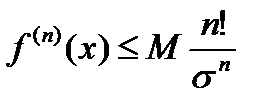
§ 4 Примеры разложения основных элементарных функций в ряд Тейлора.
Найдем разложение основных элементарных функций в ряд Тейлора в окрестности точки 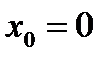 , то есть в ряд вида
, то есть в ряд вида
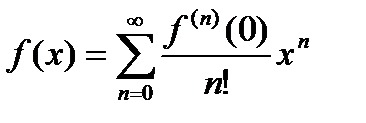 (20.11)
(20.11)
который называется рядом Маклорена. Заметим, что коэффициенты 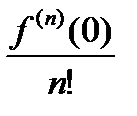 разложения (20.11)для основных элементарных функций найдены.
разложения (20.11)для основных элементарных функций найдены.
 2015-03-07
2015-03-07 1455
1455
