2015-03-07
666
Пусть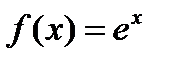 
, тогда 
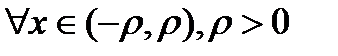выполняется неравенство:
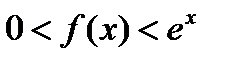
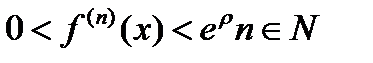
По теореме (20.4) ряд (20.11) для функции 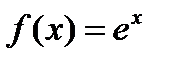сходится к этой функции на интервале 
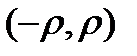при любом 
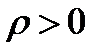, то есть радиус сходимости этого ряда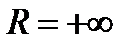 
Так как для функции 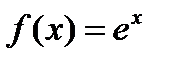выполняются равенства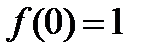 
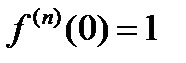для любого 
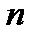, то по формуле (20.11) получаем разложение в ряд Маклорена показательной функции.
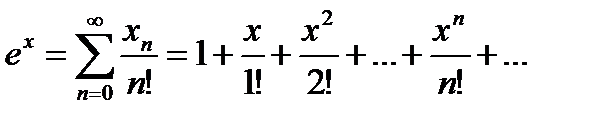(20.12)
Используя разложение (20.12)и формулы:
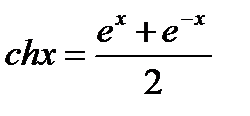
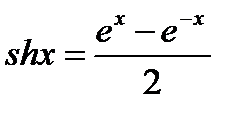
находим разложения в ряд Маклорена гиперболического косинуса и гиперболического синуса:
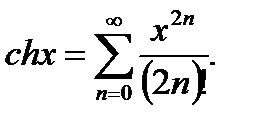(20.13)
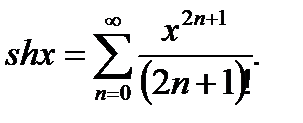(20.14)
