2015-03-07
736
Определение 22.3. Функциональный ряд вида
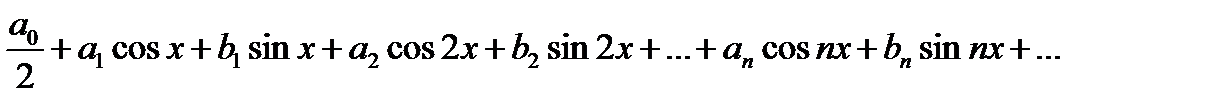
или ряд вида:
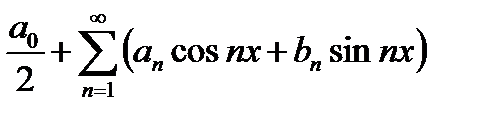(22.3)
Называется тригонометрическим рядом.
Постоянные числа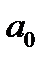 
, 
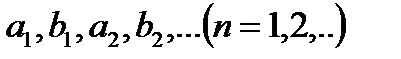называются коэффициентами тригонометрического ряда. Его частичные суммы являются линейными комбинациями, входящих в систему
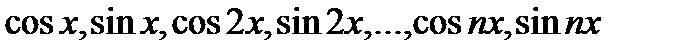(22.4)
то есть
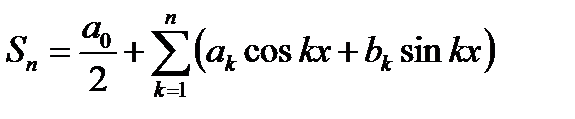(22.5)
Тригонометрический ряд (22.3) можно записать и в виде суммы простых гармоник. Действительно, объединяя слагаемые с одинаковой частотой
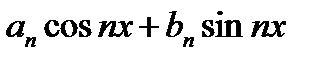
Пологая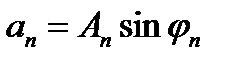 
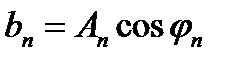получим
= 
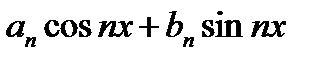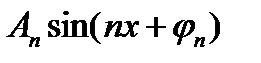
Запись в таком виде удобно в тех случаях, когда нужно знать амплитуду и начальную фазу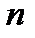 
-ой гармоники. При этом
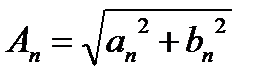и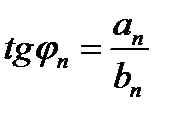 
Тогда ряд (22.3) принимает вид
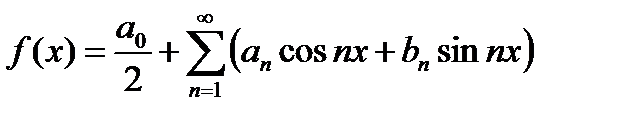(22.6)
Пусть теперь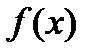 
-произвольная периодическая функция с периодом 
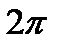. Постараемся разложить эту функцию в тригонометрический ряд в виде (22.6). в дальнейшем мы установим условия, при которых это возможно.
Поскольку эта функция имеет период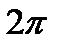 
, то ее можно рассматривать в любом интервале длины 
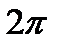. Выберем в качестве основного интервала 
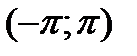: на других участках оси ОХ функция 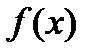будет повторять свои значения и свое поведение в основном интервале .
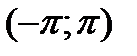Выведем соотношения, с помощью которых будем отыскивать коэффициенты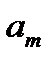 
и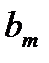 
.
Лемма 22.1. Тригонометрическая система (22.4) обладает следящими свойствами:
1.Интеграл по отрезку 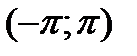, от произведения двух различных функций входящих в него, равен нулю(это свойство называется ортогональностью системы(22.4)), то есть
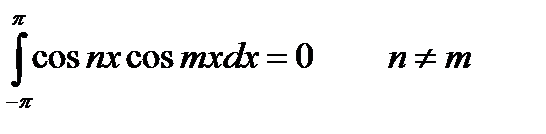
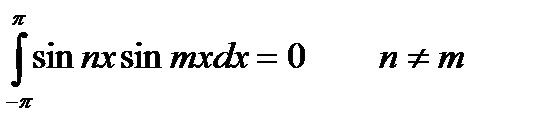(22.7)
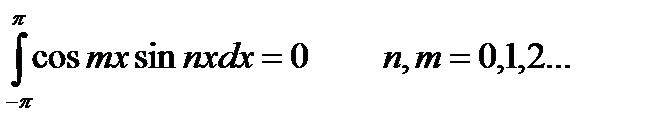
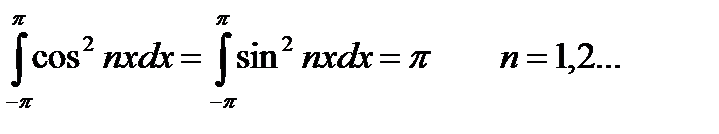(22.8)
Доказательство:
При любых целых неотрицательных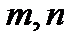 
таких, что 
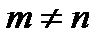, имеем:
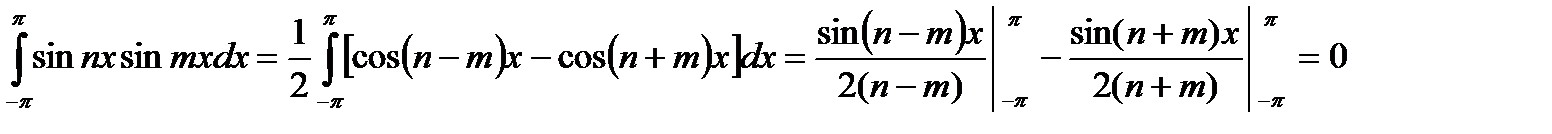
Аналогично доказываются и два других неравенства (22.7).
Докажем теперь (22.8)
Теорема 22.1. Пусть
(22.9)
И ряд, стоящий в правой части этого равенства, сходится равномерно на отрезке . Тогда
(22.10)
Доказательство: Поскольку ряд стоящий в правой части равенства (22.9) сходится равномерно на отрезке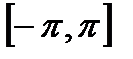 
, а все его члены являются непрерывными на этом отрезке функциями, то его сумма 
непрерывна на отрезке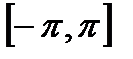 
, а сам ряд может почленно интегрировать от 
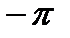до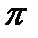 
:
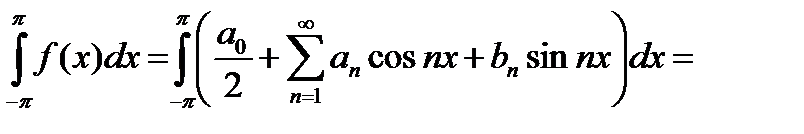
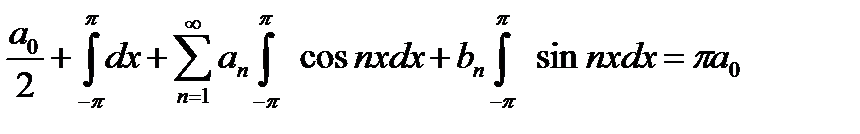
Если ряд (22.9) почленно умножить на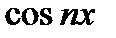 
и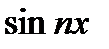 
(n=1,2,3,…), то полученные ряды будут также равномерно сходится на отрезке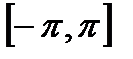
Интегрируя почленно эти ряды и используя свойство ортогональности (22.7) тригонометрической системы и равенства (22.8), будем иметь:
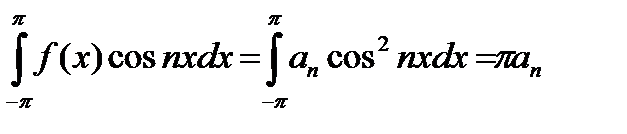
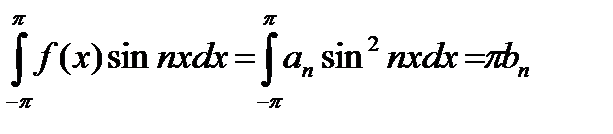
Определение 22.4. Пусть функция абсолютно интегрируема на отрезке 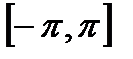. Тригонометрический ряд (223), коэффициенты которого задаются формулами (22.10), называются рядом Фурье или более подробно, тригонометрическим рядом Фурье, а числа 
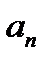и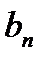 
-коэффициентами Фурье функции .
В этом случае пишут:
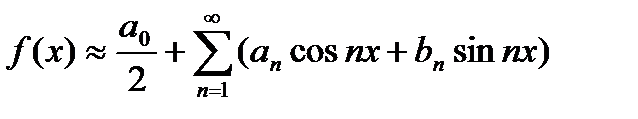
Мы уже отмечали, что сумма ряда Фурье функции есть периодическая функция с периодом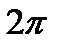 
. Если ряд сходится в интервале 
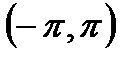, то он сходится и при всех остальных значениях 
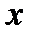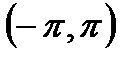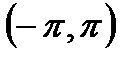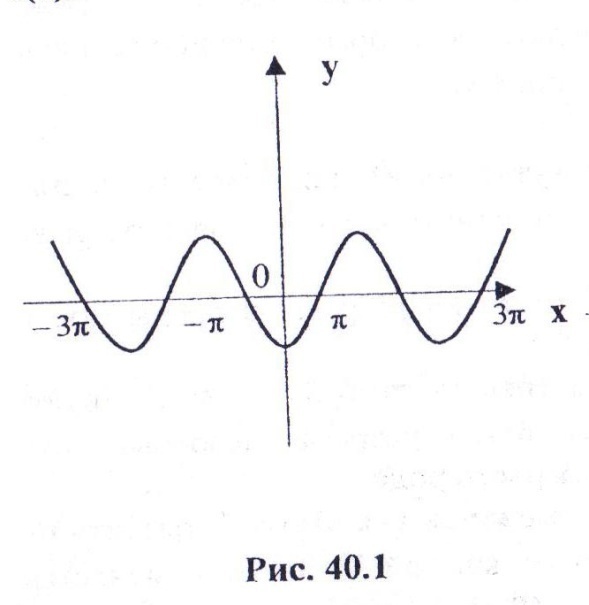
и сумма его периодически повторяет те значения, которые она принимает в основном интервале и периодически продолженную на всю числовую ось. Поэтому говоря в дальнейшем о разложении в ряд Фурье функции, заданной в интервале , мы всегда будем считать, что речь идет о периодической функции. Если при этом значения функции на концах основного интервала равны между собой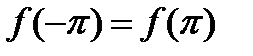 
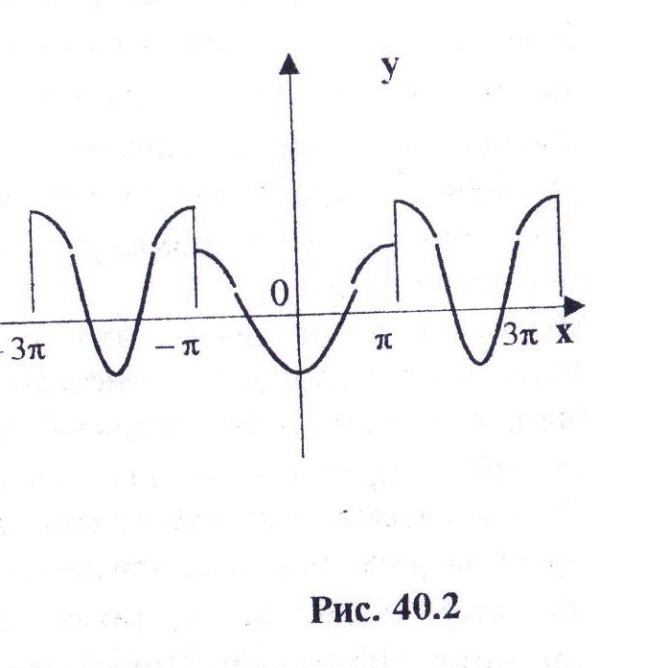
, то функция продолжается непрерывно. (рис 40.1), а если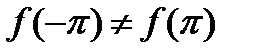 
, при таком продолжении концы основного интервала будут вялятся точками разрыва функции(рис 40.2). но мы еще не можем утверждать, что образованный ряд Фурье сходится и что его сумма равна функции .
