Гармонические колебания

Тригонометрические функции имеют важные применения в математике, в естествознании и в технике. Они встречаются там, где приходится иметь дело с периодическими явлениями, то есть явлениями, повторяющимися в одной и той же последовательности и в одном и том же виде через определенные интервалы аргументов.

Определение 22.1. Функция 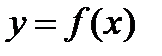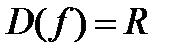называется периодической, если существуют такое постоянное число 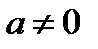, что от прибавления его к любому значению аргумента, значение функции не изменяется, то есть

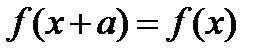
Если функция периодическая, то имеют место также неравенства

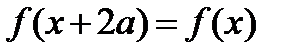
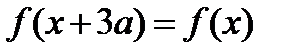
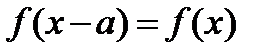
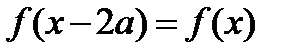
И вообще

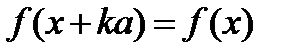
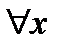и для произвольного целого

Определение 22.2. Наименьшееположительное число, от прибавления которого к любому значению аргумента значение функции не изменяется, называется периодом функции.

Например: тригонометрические функции

1, cos x, sin x, cos 2x, sin 2x, …

Имеют период :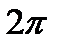

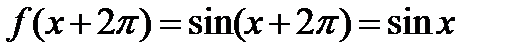
Одной из важных периодических функций являются гармонические колебания, в которых расстояние 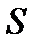колеблющейся точки от положения равновесия является функцией времени :

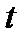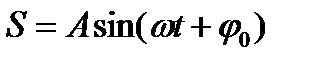(22.1)

Эту функцию называют синусоидальной. Постоянное число А предстоавляет собой то найбольшее значение, которой может достигнуть 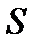. Аргумент синуса 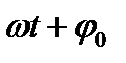называется фазой колебания, а число 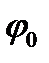равное значения фазы при 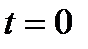-начальной фазой. Наконец 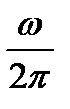называется частотой колебания.

Происхождение последнего термина делается ясным из связи между 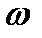и периодом Т нашей функции (периодом колебания)

Функция 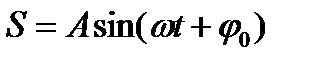периодическая, ее период Т равен 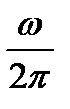, так как для увеличения фазы на 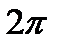нужно к независимой переменной 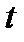прибавить 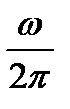,. Поэтому 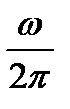= 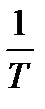, и значит, число 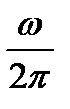показывает, сколько периодов укладывается в единице времени, то есть сколько раз данное периодическое явление повторяется в течении единицы времени: это число дает, следовательно, именно частоту явления. Число 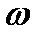показывает, сколько раз явление повторится за 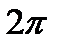единиц, его называют круговой частотой.

Для того чтобы построить график синусоидальной функции 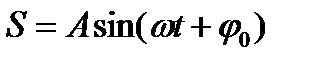, запишем эту функцию в виде

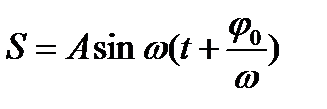
и применим для построения графика этой функции.

Колебания описываемые уравнением (22.1) называются гармоническими колебаниями, а их графики –простыми гармониками. Часто встречаются суммы простых колебаний вида:

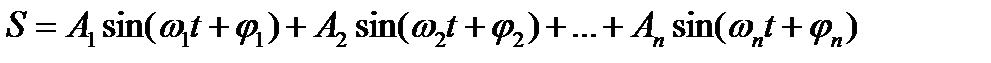(22.2)

где 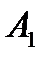, , 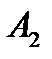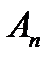-постоянные.

Колебания получающиеся в результате сложения нескольких простых гармонических колебаний, называется сложными гармоническими колебаниями, а их графики –сложными гармониками.

Заметим, что (22.2) при различных значениях параметров 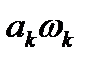и целых чисел 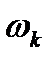и 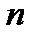приводят к самым разнообразным периодическим функциям. В терминах механики это означает, что наложение простых гармонических колебаний создает разнообразные периодические движения, отнюдь не похожие на простые гармонические колебания.

Естественно возникает обратная задача. Нельзя ли так подобрать простые гармонические колебания, чтобы их наложение вызвало заранее данное периодическое движение, как сложное гармоническое колебание?

Оказалось, что этого, вообще говоря, сделать нельзя, если ограничится последней суммой простых гармоник. Если же привлечь к рассмотрению бесконечные суммы простых гармоник, то есть ряды, то практически любую периодическую функцию можно разложить на простые гармоники.

К рассмотрению этой задачи мы сейчас и приступим.