В этом параграфе мы рассмотрим некоторые факты, относящиеся функциям комплексной переменной.
Пологая, что читатель знаком с алгеброй комплексных чисел из курса элементарной математики, только кратко напомним ее основные положения.
Пусть дано комплексное число z=x+iy, где х и у – действительные числа, а 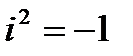 ; х называется действительной частью, а у – мнимой частью комплексного числа z.
; х называется действительной частью, а у – мнимой частью комплексного числа z.
Число z=x-iy называется сопряженным z.
Геометрически, комплексное число изображается точкой плоскости, снабженной системой декартовых координат, причем абсциссой точки служит действительная, а ординатой – мнимая часть числа. Поэтому ось абсцисс называют действительной осью, а ось ординат – мнимой осью плоскости же называют плоскостью комплексных чисел или комплексной плоскостью.
Если точка изображает число z, то ее называют точкой z. Можно изображением комплексного числа считать также радиус –вектор указанной точки. Ясно, что длина радиус – вектора равна модулю числа. Точка 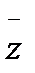 , симметрична точке z относительно действительной оси.
, симметрична точке z относительно действительной оси.
Если перейти по обычным формулам к системе полярных координат, обозначив их через 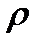 и
и 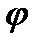 , то очевидно, будем иметь:
, то очевидно, будем иметь:
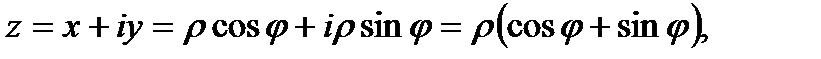
где 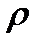 - модуль числа z, то есть
- модуль числа z, то есть
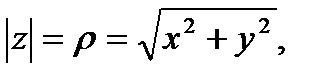 (21.13)
(21.13)
а 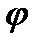 - аргумент числа z:
- аргумент числа z: 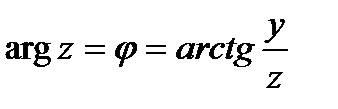 .
.
По заданному комплексному числу его аргумента находится не однозначно, а с точностью до целого числа полных оборотов. Выражение в правой части(21.13) называется тригонометрической формой комплексного числа.
Если у=0, то комплексное число z=х есть действительное число, изображаемое точкой действительной оси, а если х=0, то z=iy называется чисто мнимым числом, изображенным точкой мнимой оси.
Арифметические операции над комплексными числами проводят в соответствии с формулами:
1. 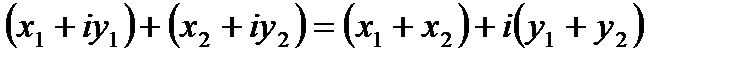
2. 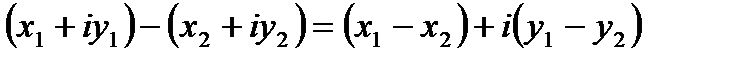
3. 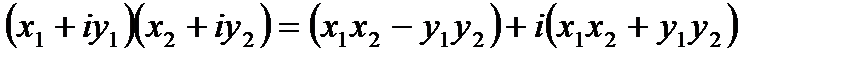
Это правило не соответствует ни одному из умножений векторной алгебры. Если сомножители взять в тригонометрической форме, то легко вывести, что
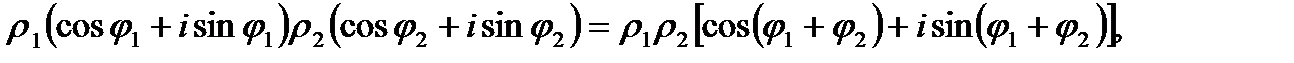
То есть при умножении модули чисел перемножаются, а аргументы складываются.
Для любого целого положительного числа n имеет место формула Муавра:
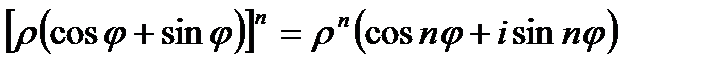
4. 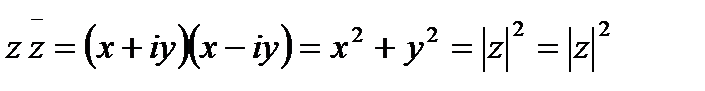
5. 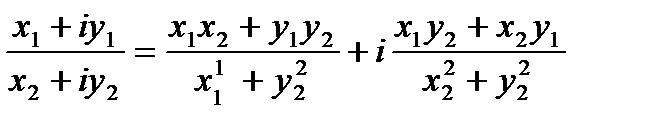 ,
, 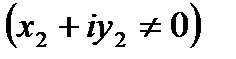
Деление есть действие, обратное умножению. Если делимое и делитель взять в тригонометрической форме, то:
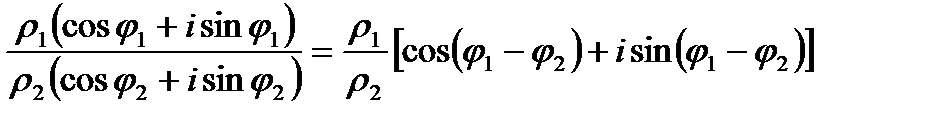
То есть при делении модуль делимого делится на модуль делителя, а аргумент делителя вычитается из аргумента делимого.
Таким образом, арифметические действия над комплексными числами производится по обычным правилам действий над обыкновенными двучленами (х+iy), но в результате 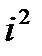 везде заменяется на -1.
везде заменяется на -1.
Комплексная величина z=x+iy называется переменной, если она принимает различные численные(комплексные) значения.
Определение21.1. Комплексная величина 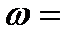 U+iV есть функция независимой комплексной переменной z=x+iy, если каждому значению этой переменной, принадлежащему некоторой совокупности комплексных чисел, называемой областью определения функции, соответствует одно или несколько определенных значений величины
U+iV есть функция независимой комплексной переменной z=x+iy, если каждому значению этой переменной, принадлежащему некоторой совокупности комплексных чисел, называемой областью определения функции, соответствует одно или несколько определенных значений величины 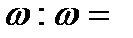 ƒ(z).
ƒ(z).
Теория степенных рядов, изложенных в предыдущих лекциях, без всяких существенных изменений справедлива и для степенных рядов в области комплексных чисел.
По определению положим:
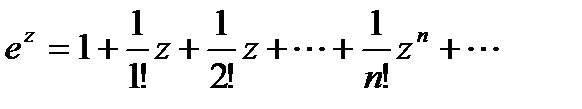
Для функции 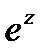 , определенной таким образом, остается справедливым основное свойство показательной функции
, определенной таким образом, остается справедливым основное свойство показательной функции
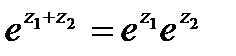
Если у=0, то есть z=x, то 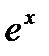 есть известная экспоненциальная функция
есть известная экспоненциальная функция 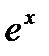 . Посмотрим теперь, как можно выразить функцию
. Посмотрим теперь, как можно выразить функцию 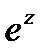 , если х=0, то есть z=iy, где у- действительное число. Имеем:
, если х=0, то есть z=iy, где у- действительное число. Имеем:
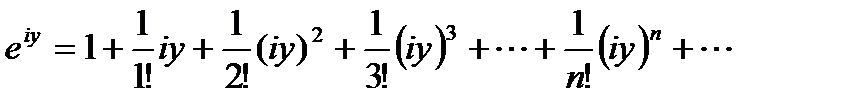
то есть
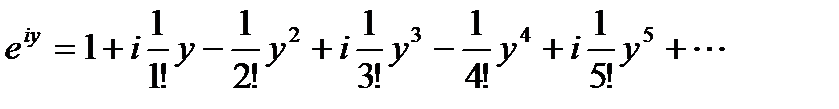
или
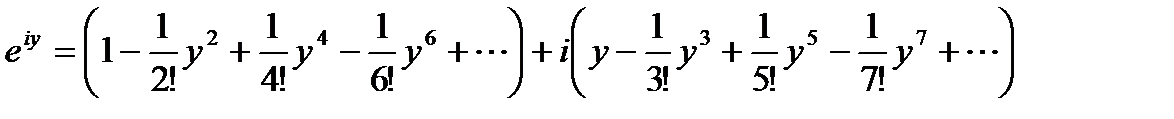
Но ряды, стоящие в скобках, представляют соответственно cosy и siny,. поэтому
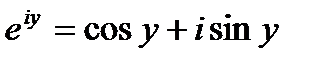
Эта формула называется формулой Эйлера.
Нетрудно заметить, что
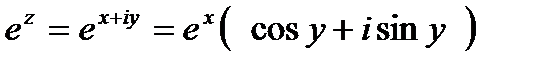
С помощью формулы Эйлера, любое комплексное число можно записать в показательной форме
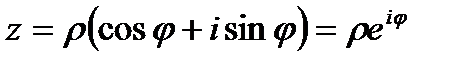
Заметим, что если 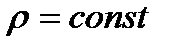 , а
, а 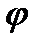 пробегает все значения от 0 до
пробегает все значения от 0 до 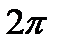 , то точка z обходит один раз окружность радиуса
, то точка z обходит один раз окружность радиуса 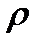 против часовой стрелки.
против часовой стрелки.
Заменив в формуле Эйлера
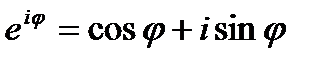 (21.14)
(21.14)
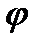 на -
на - 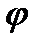 . Тогда
. Тогда
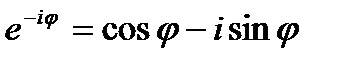 (21.15)
(21.15)
Из двух равенств(21.14) и (21.15) найдем
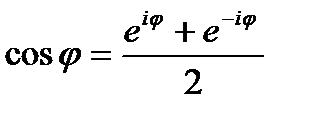
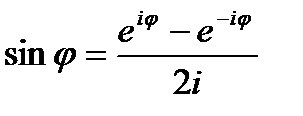
Эти формулы также называются формулами Эйлера. Они выражают тригонометрические функции через показательные.
Если в этих формулах заменить 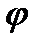 на комплексное число z, то мы получим тригонометрические функции комплексной переменной:
на комплексное число z, то мы получим тригонометрические функции комплексной переменной:
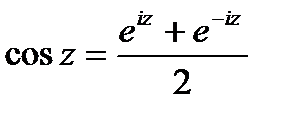 ;
; 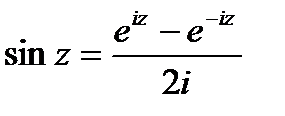 .!
.!
Заметим что, показательные, гиперболические и тригонометрические функции комплексного переменного Z определяются соответственно формулами
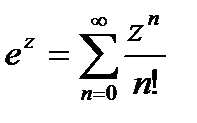 (21.16)
(21.16)
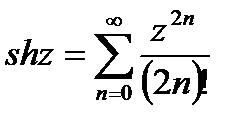 (21.17)
(21.17)
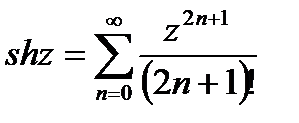 (21.18)
(21.18)
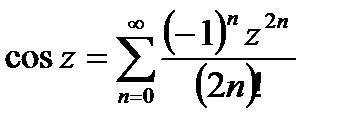 (21.19)
(21.19)
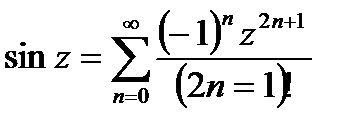 (21.20)
(21.20)
 2015-03-07
2015-03-07 3017
3017