В этом параграфе мы сформулируем условия, при которых ряд Фурье функции  сходится и имеет своей суммой именно функцию
сходится и имеет своей суммой именно функцию  . Введем предварительно несколько определений.
. Введем предварительно несколько определений.
Определение 22.4. Функция  называется кусочно монотонной на отрезке
называется кусочно монотонной на отрезке 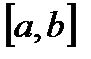 , если этот отрезок можно разбить конечным числом точек
, если этот отрезок можно разбить конечным числом точек 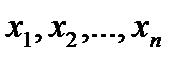 на
на 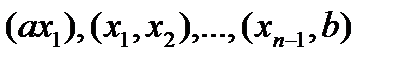 так, что на каждом из интервалов функция монотонна, то есть либо возрастающая, либо не убывающая.
так, что на каждом из интервалов функция монотонна, то есть либо возрастающая, либо не убывающая.
Из определения следует, что если функция  кусочно монотонная и ограничена на отрезке
кусочно монотонная и ограничена на отрезке 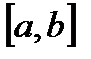 , то она может иметь только точки разрыва первого рода. Действительно, если
, то она может иметь только точки разрыва первого рода. Действительно, если 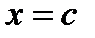 есть точка разрыва функции
есть точка разрыва функции  , то в силу монотонности функции существуют пределы:
, то в силу монотонности функции существуют пределы:
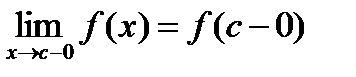
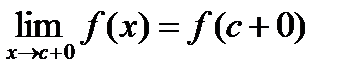 (22.11)
(22.11)
То есть точка с есть точка разрыва первого рода.
Определение 22.5 Функция  называется гладкой в интервале
называется гладкой в интервале 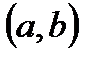 , если в этом интервале она непрерывна вместе со своей первой производной
, если в этом интервале она непрерывна вместе со своей первой производной 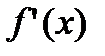 .
.
Определение 22.6. Функция  называется кусочно гладкой в интервале
называется кусочно гладкой в интервале 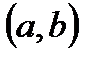 , если интервал
, если интервал 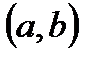 можно разбить на конечное число частичных интервалов, в каждом из которых
можно разбить на конечное число частичных интервалов, в каждом из которых  -гладкая функция.
-гладкая функция.
Таким образом, ряд Фурье функции  будет сходится и его сумма будет равно
будет сходится и его сумма будет равно  , если только сделать некоторые ограничительные предположения относительно функции
, если только сделать некоторые ограничительные предположения относительно функции  .
.
Предположим во –первых:
Что функция  , заданная на промежутке
, заданная на промежутке 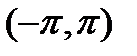 , или непрерывна, или имеет внутри этого промежутка лишь конечное число точек разрыва непрерывности.
, или непрерывна, или имеет внутри этого промежутка лишь конечное число точек разрыва непрерывности.
Мы предположим далее, что все эти точки разрыва непрерывности обладают следующими свойствами:
Если 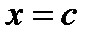 есть точка разрыва непрерывности
есть точка разрыва непрерывности  , то существуют конечные (22.11). также точки разрыва непрерывности обычно называются точками разрыва первого рода.
, то существуют конечные (22.11). также точки разрыва непрерывности обычно называются точками разрыва первого рода.
Предположим наконец, что весь промежуток 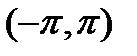 можно разбить на конечное число частей, таких, что в каждой части
можно разбить на конечное число частей, таких, что в каждой части  меняется монотонно (смотрите определение 22.4) Указанные выше условия называются обычно условиями Дирихле, то есть говорят что функция удовлетворяет условиям Дирихле в промежутке
меняется монотонно (смотрите определение 22.4) Указанные выше условия называются обычно условиями Дирихле, то есть говорят что функция удовлетворяет условиям Дирихле в промежутке 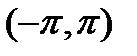 , или непрерывна в этом промежутке, или имеет конечное число разрывов первого рода, и если, кроме того промежуток
, или непрерывна в этом промежутке, или имеет конечное число разрывов первого рода, и если, кроме того промежуток 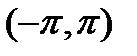 можно разбить на конечное число таких промежутков, в каждом из которых функция
можно разбить на конечное число таких промежутков, в каждом из которых функция  меняется монотонно.
меняется монотонно.
Заметим далее, что на конце 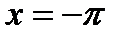 нам важен лишь тот предел, к которому стремится
нам важен лишь тот предел, к которому стремится  при
при 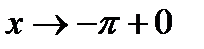 , а поэтому вместо
, а поэтому вместо 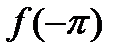 мы будем писать
мы будем писать 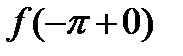 и точно также вместо
и точно также вместо 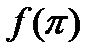 мы будем писать
мы будем писать 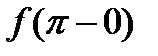
Отметим, что пределы эти могут быть конечно, одинаковы при 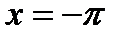 и
и 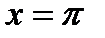 в силу периодичности функции (22.4)
в силу периодичности функции (22.4)
Одним из основных теорем теории Фурье является следующая теорема:
 2015-03-07
2015-03-07 2034
2034








