На отрезке 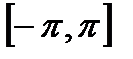 , найти тригонометрический ряд Фурье функции
, найти тригонометрический ряд Фурье функции 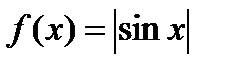 .
.
Решение.
Эта функция получается при четном продолжении функции 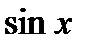 из интервала
из интервала 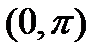 в интервале
в интервале 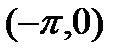
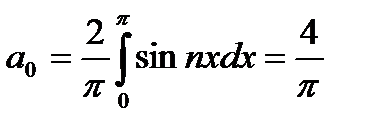
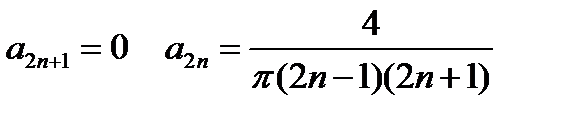
Следовательно,
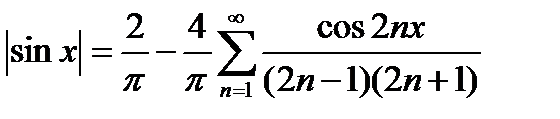
Функцию 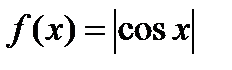 получаем из предыдущей переносом начала отсчета
получаем из предыдущей переносом начала отсчета
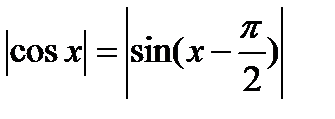
Поэтому:
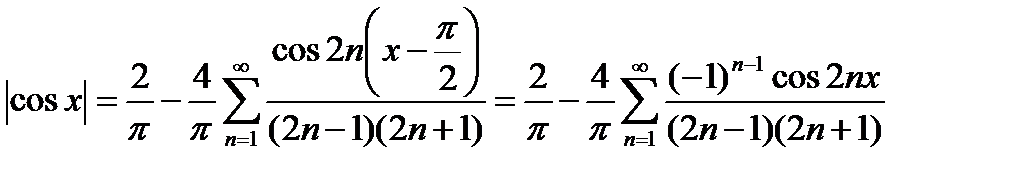
Пример 22.3 Найти на отрезке 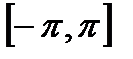 тригонометрический ряд Фурье функции:
тригонометрический ряд Фурье функции:
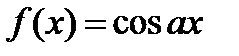
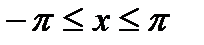
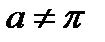
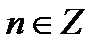
И исследовать сходимость полученного ряда.
Решение.
Продолжая функцию  периодически на всю вещественную прямую получаем непрерывную и
периодически на всю вещественную прямую получаем непрерывную и 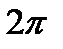 -периодическую функцию, имеющую в каждой точке обе односторонние производные(рис 40.4).
-периодическую функцию, имеющую в каждой точке обе односторонние производные(рис 40.4).
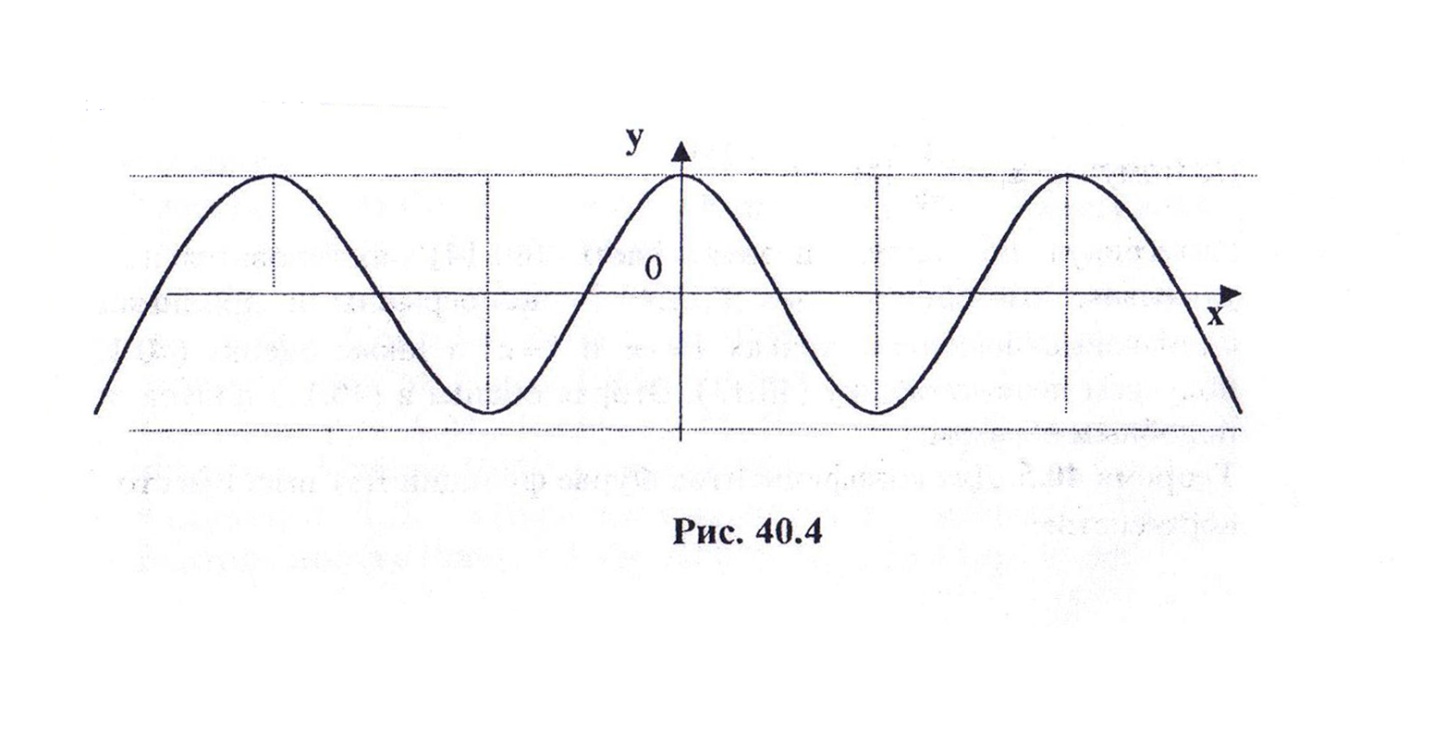
Ряд Фурье такой функции будет в любой сходится к значению функции в этой точке. Найдем коэффициенты Фурье. Так как функция четная, то все коэффициенты 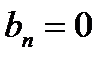 , а
, а 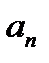 вычисляются следующим образом:
вычисляются следующим образом:
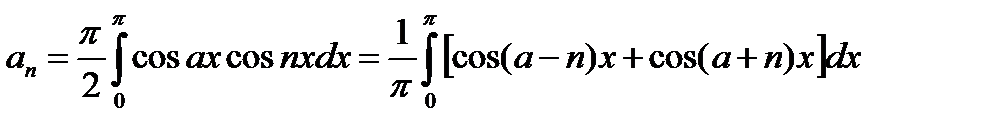 =
= 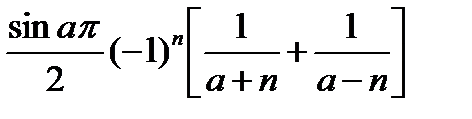
Откуда
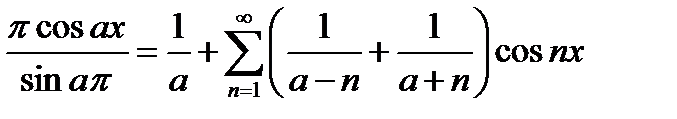
 2015-03-07
2015-03-07 730
730








