Интегрируя по частям и учитывая, что 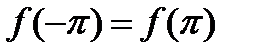 , имеем
, имеем
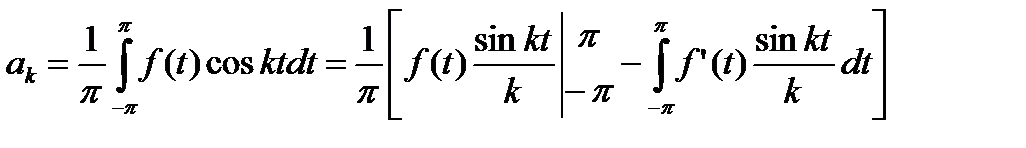 =
= 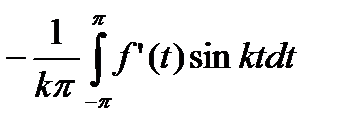 (22.14)
(22.14)
Поэтому: 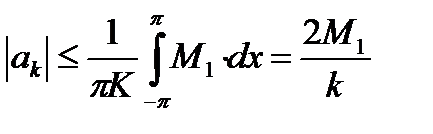
Интегрируя по частям правую часть (22.14) последовательно и учитывая, что производные непрерывны и принимают одинаковые значения в точках 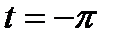 и
и 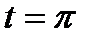 , а также оценку (22.12) получаем первую оценку (22.13). вторая оценка в (22.13) получается подобным образом.
, а также оценку (22.12) получаем первую оценку (22.13). вторая оценка в (22.13) получается подобным образом.
Теорема 22.5. Для коэффициентов Фурье функции  имеет место неравенство:
имеет место неравенство:
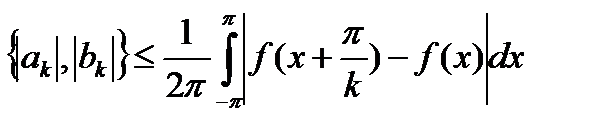 (22.15)
(22.15)
Теорема 22.6. Теорема Римана. Пусть функция  аюсолютно интегрируема на конечном интервале (a,b). Тогда
аюсолютно интегрируема на конечном интервале (a,b). Тогда
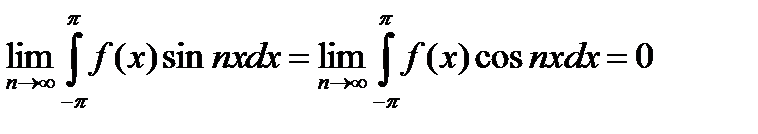
 2015-03-07
2015-03-07 692
692








